Какой цифрой оканчивается произведение 21 множителя каждый из которых равен: Какой цифрой оканчивается произведение 21 множителя, каждый из которых равен n, если n =5,6,4,2,3? А если множителей

Своя игра. Степень с натуральным показателем

1. СВОЯ ИГРА

2. Нестандартный урок Алгебра 7 класс

Тема: «Степень с натуральным показателем»
Учитель: Смирнова Екатерина Алексеевна
Творческая группа: Воеводина Алина
Терняева Анна
Гаспарян Грета
Кондратова Ангелина
Елисеева Полина
Предмет математики
настолько серьезен,
что полезно не упустить
Блез Паскаль
(1623 – 1662 гг.)
Французский математик,
физик, религиозный философ
и писатель
случая сделать его
немного занимательным.

4. Правила игры:

• Игра состоит из 3х раундов: 1 раунд и 2 раунд
состоят из 5 тем каждый. В теме – 5 вопросов.
Вопросы располагаются слева направо по
возрастанию степени сложности.
• В 1 раунде стоимость вопросов от 2х до 8
баллов, во 2 раунде- от 3х до 10 баллов. На
обсуждение дается от 30 секунд до 2х минут.
Для проведения игры класс разбит на две
команды. Игра начинается с жеребьёвки.
Победившая команда первой выбирает
задание.
• Выбор темы и вопроса осуществляет
капитан. В первом раунде ответ на вопрос
дает выбранный капитаном член команды
или сам капитан. Во 2 раунде капитан после
выполнения задания поднимает сигнальную
карту и сдает решение жюри. Выполняют
задания обе команды. Если команда,
выбиравшая вопрос, выполнила задание
неверно, то 2 команда дает ответ на вопрос.
Если её ответ верен, то она получает баллы.
• После каждого раунда жюри подводит
итоги. Во 2 раунде игру начинает команда,
набравшая в 1 раунде больше баллов.
• В финальном раунде команды делают ставку
в пределах 20 баллов, записывают её на
бумаге и сдают жюри.
• Капитаном с помощниками дается задание
«Дидактическая игра».
• Выполнив задание, капитаны с
помощниками сдают решение жюри и
присоединяются к командам, которые в это
время решают кроссворд по теме «Степень
с натуральным показателем».
• Правильный ответ в финальном раунде
увеличивает общую сумму команды на
сделанную ставку, а неверный – уменьшает.
• Жюри подсчитывает баллы и оглашает
результаты.
• Выигрывает команда, набравшая больше
число баллов!

9. Формула успеха

«Мы помножим ум и ловкость,
К ним прибавим оптимизм,
С нашей формулой успеха –
Вся и всех мы победим!»

10. Коэффициент удачи

КОЭФФИЦИЕНТ УДАЧИ
Будем мыслить, рассуждать
И конечно побеждать!
А удача улыбнётся,
Только тем, кто не сдаётся!

11. ЦЕЛИ:

Повторение и систематизация материала темы;
Формирование умения применять приемы
сравнения, переноса знаний в измененную
нестандартную ситуацию;
Развитие мышления, эрудиции, интуиции,
любознательности;
Формирование интереса к предмету;
Воспитание активности, трудолюбия,
целеустремленности, коллективизма.

12. Рефлексия – умение человека осознавать, что он

делает, и аргументировать, обосновывать свою
деятельность.
• Выбери из предложенных рисунков тот, который
соответствует твоему настроению на начало урока
и отметь его галочкой(✓).
Мне хорошо,
я готов к уроку.
Мне безразлично.
Я тревожусь,
всё ли у меня получится.

13. Жеребьевка.

Горело 5 свечей, 2 погасли. Сколько свечей
осталось?
В семье 5 сыновей и у каждого есть сестра.
Сколько детей в семье?
• Врач прописал больному 3 укола: по уколу
через каждые полчаса. Сколько потребуется
времени, чтобы сделать все уколы?
• В темноте девочка увидела 6 пар кошачьих
глаз. Сколько пар ног у этих кошек?
• Как изменится дробь, если её числитель
увеличить на знаменатель?

14. Ответы:

•2
•6
• 1 час
• 12
• на 1
Знаю теорию
2
3
4
5
6
2
3
4
5
6
Умею логически
мыслить (верно
ли
утверждение?)
2
3
5
6
8
Знаю историю
математики
2
3
4
5
6
Считаю устно
2
3
4
5
6
Знаю свойства
Сформулировать определение степени
числа а с натуральным показателем n,
большим 1.
Ответ: степенью числа а с
натуральным показателем n,
большим 1, называется
выражение аn, равное
произведению n множителей,
каждый из которых равен а.
Сформулировать определения степени числа
а с показателем 1 и показателем 0.
Ответ: степенью числа а с
показателем 1 называется само
число а. Степень числа а, не
равного нулю, с нулевым
показателем равна единице. 00
не имеет смысла.
Сформулировать определение одночлена.
Ответ: выражения, которые
являются произведениями
чисел, переменных и их
степеней называют
одночленами.
Сформулировать определения степени числа
а с показателем 1 и показателем 0.
Ответ: степенью числа а с
показателем 1 называется само
число а. Степень числа а, не
равного нулю, с нулевым
показателем равна единице. 00
не имеет смысла.
Сформулировать определение
одночлена стандартного вида.
Ответ: одночлен, записанный
в виде произведения
числового множителя,
стоящего на первом месте и
степеней различных
переменных, называют
одночленом стандартного
вида.
Сформулировать определение степени
одночлена.
Ответ: степенью одночлена
называют сумму показателей
степеней всех входящих в него
переменных. Если одночлен не
содержит переменных и является
числом, отличным от нуля, то
степень этого одночлена считают
равной 0.
Заполните пропуски. Сформулируйте
соответствующее правило.
am . an = …
Ответ: am . an = am+n, а – любое число
m и n – произвольные натуральные
числа.
При умножении степеней с
одинаковыми основаниями
основание оставляют прежним, а
показатели степеней складывают.
Заполните пропуски. Сформулируйте
соответствующее правило.
am : an = …
Ответ: am : an = am-n, а ≠ 0; m и n –
натуральные числа, m > n.
При делении степеней с
одинаковыми основаниями
основание оставляют прежним, а
из показателя степени делимого
вычитают показатель степени
делителя.
Заполните пропуски. Сформулируйте
соответствующее правило.
(am)n = …
Ответ: при возведении степени в
степень основание оставляют
тем же, а показатели
перемножают.
(аm)n = amn, a – любое число,

m и n – произвольные
натуральные числа.
Заполните пропуски. Сформулируйте
соответствующее правило.
(abc)n = …
Ответ: Чтобы возвести в степень
произведение достаточно
возвести в эту степень каждый
множитель и результаты
перемножить.
(abc)n = anbncn
a,b,c- любые числа,
n – натуральное число
Заполните пропуски. Сформулируйте
соответствующее правило.
an . bn = …
Ответ: При умножении степеней с
разными основаниями и
одинаковыми показателями
основания перемножают, а
показатель оставляют тем же.
an . bn = (ab)n, a и b – любые числа, а
n – произвольное натуральное число.
Верно ли утверждение?
Если квадраты двух чисел равны, то
равны и сами числа.
Ответ: нет,
например: (-5)2 = 52; -5 ≠ 5.
Верно ли утверждение?
Если кубы двух чисел равны, то равны и
сами числа.
Ответ: да.
Верно ли утверждение?
Квадрат натурального числа может
оканчиваться любой цифрой.
Ответ: нет, может оканчиваться
только 0; 1; 4; 9; 6; 5.
Верно ли утверждение?
Четвертая степень натурального числа
может оканчиваться только одной из
цифр 0; 1; 5; 6.
Ответ: да.
Верно ли утверждение?
Если к отрицательному числу прибавить
его квадрат, то получится положительное
число.
Ответ: нет,
например: -0,1+(-0,1)2=
= -0,1+0,01 = -0,09.
Какой математик впервые ввел
современную запись степени х3; х10 ?
Ответ: Рене Декарт,
французский математик.
Происхождение слова «алгебра».
Ответ: слово «алгебра»
арабского происхождения;
термин «аль-джебр» взят из
названия книги
среднеазиатского ученого
Мухаммеда из Хорезма
(9 век).
Кому принадлежат слова:
«Математика – царица наук,
арифметика – царица математики»?
Ответ: Карлу Гауссу,
немецкому математику 19
века, «королю» математиков.
Каким математиком впервые введены
термины «абсцисса», «ордината»,
«координата»?
Ответ: впервые введены
немецким математиком
Готфридом Лейбницем
в XIX веке.
Самая древняя «счётная машина».
Ответ: пальцы рук и ног,
камешки и другие мелкие
предметы.
Вычислите:
102 — 32
Ответ: 100 – 9= 91.
Вычислите:
(-½)5 . 8
Ответ: —
.
8 = -¼.
Вычислите:
0,2515 . 415
Ответ: (0,25 . 4)15 = 1.
Вычислить:
9 . 75
7
—————-496
14
7
——-Ответ: 712 = 72 = 49.
Вычислите:
-62 – (-1)4
Ответ: -36 – 1 = -37
Упражнения
3
5
6
8
10
Задачи
3
5
7
8
10
Вычислить
3
4
5
6
8
Уравнения
3
5
7
9
10
Преобразование
выражений
3
5
7
8
10
Сравнить числа:
а) (-2,4)4 и (-5,2)3
б) -6,82 и -5,72
Ответ: (-2,4)4 > (-5,2)3 , так как
(-2,4)4 > 0, а (-5,2)3
-6,82 5,72
Заменить М одночленом так, чтобы
получилось тождество
М2 . 12х6 = 108х8
Ответ: М = ±3х
М2 = 108х8 :
(12х6)
М2 = 9х2
М = ±3х
Поставить вместо пропущенных выражений
такие, чтобы получилось тождество.
(….) 2 . (….) 3 = -27b 11
Ответ: b4 и -3b
Докажите, что число 196374 + 391 164 – 2
делится на 5
Ответ: 196 374 оканчивается
цифрой 6
391 164 оканчивается цифрой 1.
Данное число оканчивается
цифрой 5, следовательно
делится на 5.
Какой цифрой оканчивается число 1989 1989
Ответ: 1989 1 оканчивается
цифрой 9
1989 2 оканчивается цифрой 1
1989 3 оканчивается цифрой 9
1989 4 оканчивается цифрой 1
Показатель степени – нечетное
число. Значит, число
оканчивается цифрой 9.
Как изменится площадь круга, если его
радиус уменьшить в 2 раза?
Ответ:S = ∏R 2
Уменьшится в 4 раза.
На покраску квадрата израсходовали 40 г
краски. Хватит ли 350 г краски, чтобы
покрасить квадрат, сторона которого в 3
раза больше?
Ответ:S = а 2 , площадь
увеличится в 9 раз. На покраску
израсходуют 40 . 9 = 360(г).
Краски не хватит.
Объем шара вычисляется по формуле V =
где r – радиус шара. Найти объем шара
радиуса 3 см.
округлить до целых.
Ответ:
=108(см 3)
= 4 . 3 3 ; V = 4 . 27=
,
Найти площадь кольца, если r1 = 2см, r2 =
= 4см.
округлите до целых.
Ответ:
S = 3 . 42 — 3 . 22 = 3(16-4) =
= 36 (cм2)
Бассейн, имеющий форму куба, наполняется
трубой за 40 мин. Успеют ли за 5 часов
наполнить через такую же трубу бассейн,
имеющий форму куба, ребро которого в 2 раза
больше?
Ответ: V = а 3. Объем
увеличивается в 8 раз. Времени
потребуется 40 . 8 = 320 (мин).
5 ч = 5 . 60 = 300 (мин).
Наполнить бассейн не успеют.
Ответ:
=
Ответ:
=
=1
0
Ответ: 1 + = 2,25
+5
Ответ:
=
Ответ:
Ответ:
x = 19.
Ответ:
Ответ:
Ответ:
Решите уравнение при всех значениях
параметра а.
ax = 2 — a
Ответ: при а ≠ 0
при а = 0 корней нет.
Выполните действия.
(3xy)3 × (-2x2y3)2
Ответ: 27x3y3 × 4x4y6 = 108x7y9
Запишите одночлен в стандартном виде и
найдите его значение .
3
Ответ: __ а5 =
2
16
х __ = — __
81
__ х
(-
2
__
3
) х (- __ )4 = -1 х
Представьте выражение в виде квадрата или
куба одночлена.
Ответ:
Упростить выражение
Ответ:
Вычислите:
Найти значение выражения
(5x – 3y) х 4×2 – 5×2(4x + y)
при х = ; y = -27
Ответ: 20×3 — 12x2y – 20×3 — 5x2y =
= -17x2y.
При х = ; y = -27
-17 х х (-27) = 51

73. Дидактическая игра.

• Дается 2 минуты на то, чтобы запомнить выражения,
записанные в клетках квадрата. Затем по памяти
заполнить клетки квадрата. Для того, чтобы
запомнить и правильно воспроизвести, необходимо
установить закономерность в записи выражений.
(a6b12)2
(a3b8)4
(a4b8)3
(a2b4)6
a12b24
(a2b4)6
(a6b12)2
(a3b8)4
(a4b8)3

74.

Кроссворд 6
7
9
1
8
2
3
4
5
10

По горизонтали:
1. Действие, с помощью которого вычисляются значения степени.
2. Произведение, состоящее из одинаковых множителей.
3. Действие показателей степеней при возведении степени в степень.
4. Действие степеней, при которых показатели степеней вычитаются.
5. Немецкий математик, который ввел термин «показатель степени».
По вертикали:
6. Число всех одинаковых множителей.
7. Степень с нулевым показателем.
8. Повторяющийся множитель.
5
10
9. Значение выражения :
23 ∗ 55
• 10. Показатель степени, который обычно не пишут

76. Дидактическая игра.

• Дается 2 минуты на то, чтобы запомнить выражения,
записанные в клетках квадрата. Затем по памяти
заполнить клетки квадрата. Для того, чтобы
запомнить и правильно воспроизвести, необходимо
установить закономерность в записи выражений.
(a6b12)2
(a3b8)4
(a4b8)3
(a2b4)6
a12b24
(a2b4)6
(a6b12)2
(a3b8)4
(a4b8)3

77.

Заполненный кроссворд П
О
К
Е
А
В О З В Е Д Е Н И
А
И
Т
Н
О
Е
И
С Т
Л
Ц
Ь
А
Н
О
П Р О И З В Е
А
Д Е Л Е Н И
И
Ш Т И Ф Е Л
Ч
Е
Т
Ы
Р
Е П Е Н Ь
Д
И
Д Е Н И Е
И
Е
Ц
А
ь

78. Рефлексия – умение человека осознавать, что он

делает, и аргументировать, обосновывать свою
деятельность.
• Выберите из предложенных рисунков тот, который
соответствует твоему настроению после
пройденного урока и отметь его галочкой(✓).
Мне понравилось,
я доволен собой.
Мне все равно.
Мне грустно,
я не всё усвоил.
Подведение итогов
игры!!!
Спасибо за игру!!!
«Учение, лишенное всякого интереса,
?
и взятое только силою принуждения,
убивает в ученике охоту к учению,
без которой он далеко не уйдет,
а учение, основанное только на
интересе, не дает возможности
окрепнуть самообладанию и воле
ученика, так как не все в учении
К. Д. Ушинский
интересно и придет многое,
что надобно будет взять силою воли»

Технология развивающего обучения на уроках математики

Перминова Вера Алексеевна
учитель математики МАОУ Гимназия № 17
город Белорецк,
G
Республика Башкортостан
Из опыта работы по учебнику «Математика
5 класс.», «Математика 6 класс»,
под редакцией
Дорофеев Г.В.,Петерсон Л.Г.

3. Технология развивающего обучения

.
Современные подходы к организации
системы школьного образования, в том
числе и математического образования,
определяются, прежде всего , отказом
от единообразной , унитарной средней
школы.
Направляющим вектором этого подхода
являются гуманизация и гуманиторизация
школьного образования, которая
реализуется как гуманитарная ориентация
обучения математике.
Именно поэтому в качестве основополагающего
принципа новой концепции школьного
математического образования в аспекте «математика
для каждого» на первый план выдвигается принцип
приоритета развивающей функции в обучении
математике. Иными словами, обучение математике
ориентировано не столько на собственно
математическое образование, в узком смысле слова,
сколько на образование с помощью математики.

7. Цели обучения математики

Овладение комплексом математических
знаний, умений и навыков, необходимых:
а)для повседневной жизни на высоком
качественном уровне и профессиональной
деятельности; б)для изучения на
современном уровне школьных предметов
естественно- научного и гуманитарного
циклов; в)для продолжения изучения
математики в любой из форм непрерывного
образования;
Формирование и развитие качества
мышления, необходимых образованному
человеку для полноценного
функционирования в современном обществе,
в частности, эвристического( творческого) и
алгоритмического( исполнительного)
мышления в их единстве и внутренне
противоречивой взаимосвязи;
Формирование и развитие у учащихся
абстрактного мышления и, прежде всего,
логического мышления;
Формирование математического языка и
математического аппарата как средства
описания и исследования окружающего
мира и его закономерностей, в частности,
как базы компьютерной грамотности и
культуры;
Формирование умений деятельности и
развитие у учащихся морально-этических
качеств личности, адекватных полноценной
математической деятельности;
Реализация возможностей математики в
формировании научного мировоззрения
учащихся, в освоении ими научной картины
мира.
Достичь этих целей помогает технология
развивающего обучения,которая
включает в себя обеспечение совместной или
самостоятельной учебно-познавательной
деятельности учащихся, при которой
учащиеся сами “ додумываются” до решения
ключевой проблемы урока и сами могут
обьяснить, как действовать в новых
условиях.
Остановлюсь на одном из методов ТРО
(технологии развивающего обучения)это активизация мыслительной
деятельности учащихся путем
решения развивающих задач.
Решение развивающих задач, как на
уроке, так и во внеурочное время позволяет
увлечь учащихся (пусть не всех)
математикой, что в дальнейшем дает
возможность не бояться данного предмета.
Большим помошником в этом является
учебник под редакцией Г.В.Дорофеева, Л.Г.
Петерсон.
Учителя, которые в 5 классе берут детей,
обучающихся в начальной школе по данной
программе, отмечают, что они более
самостоятельны, работоспособны, у них
лучше развито логическое мышление, речь,
познавательный интерес. Они не боятся
ошибок, нестандартных ситуаций, задают
вопросы, выдвигают гипотезы, отстаивают
свою точку зрения.
Если продолжить начатую работу в 5-6
классах, то накопленный потенциал помогает
создать прочную базу для развития
деятельных способностей детей и их
успешного обучения в старших классах.
При переходе же на традиционные учебники
их развитие замедляется, снижается
познавательный интерес.
Этого делать нельзя!
Остановлюсь на некоторых
эвристических приемах, которые
позволяют самостоятельно управлять
процессом решения творческих задач,
применений знаний в новых, необычных
ситуациях.
Эвристика
Метод проб
и ошибок
Метод
перебора
Метод
малых
изменений
Аналогия
Составление
задач
по
рисункам,
Логические
задачи.
Язык
чисел
и его алфавит

18. Метод проб и ошибок

Например:
1)Одна сторона прямоугольника на 3 см больше другой.
Площадь равна 70 кв.см.Найти стороны
прямоугольника.
Решение: Имеем математическую модель
х(х+3)=70.Подбираем решение «экспериментально».И
в одной из попыток находим х=7.Казалось задача
решена, но это не так. Необходимы дополнительные
рассуждения, хотя и совсем простые.
Если х>7,то х+3>10, значит х(х+3)>70
Если х
Равенство, данное в условии, верно только для одного
числа х=7, тогда х+3=10.
2)Продолжи ряд:
2,5,12,27,58…
8,3,18,9,28,27…

20. Метод перебора

Например:
Задумано двухзначное число , которое
на 52 больше произведения своих
цифр. Какое число задумано?
Умея записывать числа в позиционном
виде имеем 10х+у=ху+52,где х, у
цифры от 0 до 9

21. Составим таблицу 10х+у=ху+52

х
5
уравнение
50+у=5у+52
Упр.ур-ие
у
50=4у+52 невозможно
6
60+у=6у+52
8=5у
7
70+у=7у+52
6у=18
3
8
80+у=8у+52
7у=28
4
9
90+у=9у+52
8у=38
невозможно
невозможно
Таким образом задуманное число 73. либо 84.
Метод перебора можно использовать при решении
задач с целыми числами.
Например:
1) Докажите, что разность между любым
натуральным числом и суммой его цифр делится на
9.
2)К числу 43 припишите слева и справа по одной
цифре так, чтобы полученное четырехзначное число
делилось на 45.Найти все решения.

23. Метод малых изменений

Предполагает последовательное сведение заданного в условии задачи
объекта к требуемому за счет построения цепочки моделей. Каждая из
этих моделей получается в результате незначительной, т.е.
сохраняющей основные качественные характеристики самого объекта
деформации одного из его компонентов или предыдущей модели.
Такими изменениями компонентов часто пользуются при
доказательстве неравенств, сравнении величин.
Например: Докажите истинность высказывания (№356,5кл.)
1+1/2+1/3+…+1/64
(1/5+1/6
1/5
доказательству следующих высказываний
1+1/2+1/3+1/64
¼+1/5+1/6+1/7
1/8+19+1/10+1/11+…+1/15
1/16+1/17+…+1/31
1/32+. .+1/63

24. Аналогия

Это сходство между объектами. Задачи этой серии
направлены на отработку таких познавательных
приемов, как проведение словесных аналогий и
нахождение аналогий между фигурами.
Например:1) Что общего в примерах каждого
столбика? Какой пример в каждом столбике
«лишний»?
25+3*4
72-16*2
(18+12)*7
(40-12):4
18:3+24
90-45:5
(21-6)*3
(9*8):6
8*6+19
6*9-38
5*(25+47)
48:(3*8)
2)Нарисуй недостающую фигуру:

25. Составление задач по рисункам, схемам, таблицам

Это эффективное средство развития языковых способностей
школьников (то, что плохо произносится, плохо понимается),
они вносят определенное разнообразие в работу с типовыми
упражнениями курса, увлекают оригинальностью постановки и
решения, возможностью свободно мыслить и давать
неоднозначные ответы.
Например: придумай задачу по схеме, считая. Что втечении
указанного времени вид движения не изменялся. Придумай
значения переменных и найди ответ
а км/ч в км/ч
m км/ч
t=2ч
d=?
s км
a км
n км/ч
d 0,3=?

26. Язык чисел и его алфавит

Основная развивающая цель всех задач данной группы состоит
в том, чтобы подвести учащихся к осознанию того факта, что
помимо привычной для них системы счисления существуют и
другие способы наименования и записи натуральных чисел. От
решения задач на представление натуральных чисел в виде
суммы разрядных слагаемых, когда основания систем счисления
равны 10 и 2, ( причем задач как прямых, так и обратных),
учащиеся самостоятельно приходят к выводу правила перевода
натуральных чисел из одной позиционной системы счисления в
другую. Работая в двоичной системе счисления ребята
выясняют, что для изображения чисел в этой системе требуются
лишь две цифры: 0 и1, в троичной : 0,1,2 и т.д., Большинство
учащихся с удовольствием работают над этими задачами.

27.

Логические задачи Задачи этой серии не имеют прямой связи с каким-либо
учебным материалом, их можно встретить в любой теме курса
математики 5-6 класса. Они используются с целью воспитания у
школьников умения проводить доказательные рассуждения.
Многие из них могут быть решены табличным способом, таких
задач в учебнике под редакцией Петерсон, очень много, они
обозначаются буквой «С»- что означает «здесь главное – твоя
смекалка.».
Например: №101(5кл) какой цифрой заканчивается
произведение 21 множителя, каждый из которых равен 5? 2? 3?
А если множителей 1221?
№255(5кл)Когда пассажир проехал половину пути, он стал
смотреть в окно и смотрел до тех пор, пока не осталось
проехать половину от того пути, что он проехал, смотря в окно.
Какую часть всего пути пассажир смотрел в окно?

28. Наши успехи.

2007-2008 уч.год
Точилкин Кирилл-3 место (город)
Кирсанова Света-(похвал.грамота)
Королькова Элина-(похвал. грамота)
2010-2011уч год
Чеботарев Марк(6кл)-победитель(город).Победитель
республиканской математической олимпиады «МАТЛЕТ».
Устинова Алена (6кл)-призер(город), победитель Всероссийской
заочной олимпиады «Авангард»
Павочкин Ярослав(6кл) –призер Всероссийской заочной
олимпиады «Авангард»
Бармина Нина (6кл)-призер Всероссийской заочной олимпиады
«Авангард»
Мосалева Александра (5кл)- победитель (город)
Костенкова Юля (5кл)-призер (город)
Харрасова Азалия (5 кл)-призер(город)

29. Внеклассные городские мероприятия 2010-2011уч.год

5 класс- 1 место
6А класс — 1 место
Участие в городской
математической
конференции им
Л.Н.Зинченко
Чеботарев Марк «
Нумерология в судьбе
человека»
Юсупов Юсуф «Снег не
только беда…»

30. Зачеты по вертикали

31. Ежегодное участие в международной олимпиаде «Кенгуру», «Кенгуру- выпускникам.»

2007-2008 уч.год
(результаты следует признать очень
хорошими)
Точилкин Кирилл-118 баллов
Щербакова Наталья-101баллов
Бышин Артем -113 баллов
Желтова Яна 109 баллов

32.

Республиканская олимпиада «Матлет» Ученик 6 а класса
стал победителем
республиканской
олимпиады
«матлет».
Литература:
1.Методические материалы у учебникам
Г.В.Дорофеева, Л.Г. Петерсон.
(автор-составитель Кубышева М.А.
Москва 2006)
2.Математика 5, 6 класс (учебники в 3
частях Дорофеев Г.В., Петерсон Л.Г.)

Число 15 | Математика, которая мне нравится

Пишите об интересных свойствах числа . Картинки приветствуются!

Выкладываю свойства числа , которые прислал Лейб Александрович Штейнгарц.

1. Число 15 является суммой двух, а также и суммой трех последовательных чисел.

2. Число 15 является суммой пяти последовательных чисел.

3. В бильярде 15 шаров в начальной позиции складывают в виде равностороннего треугольника.

4. В Россию бильярд был завезен из Голландии Петром I. Новинка быстро завоевала популярность. После смерти Петра I обучение игре на бильярде было включено Верховным тайным советом в курс наук Петра II, его внука и наследника.

Екатерина II указом от 7 декабря 1770 года приказала на постоялых дворах “для увеселения приходящих дозволить иметь бильярды”

5. Первый бильярдный стол был изготовлен мастером Анри де Винемом в 1469 году для короля Франции.

Часто игру БИЛЬЯРД называют БИЛЛИАРДОМ. В этих двух словах в совокупности 15 букв.

6. В дополнение к предыдущим пунктам о бильярде (биллиарде) предлагаем распутать такой арифметический ребус:

Показать решение

   

7. БИЛЛИАРДОМ называется следующее число:

8. Число называется ПОЛУПРОСТЫМ, если его можно представить в виде произведения двух простых чисел. Следующие оба числа являются ПОЛУПРОСТЫМИ.

9. Число 15 является числом МЕРСЕННА, то есть оно представимо в виде .

10. Число можно разложить на простые множители следующим образом:

Как видим, в результате получаются лишь единицы и тройки, сумма которых равна 15.

11. Пятиконечная звезда, как бы составлена из 15-ти отрезков.

12. В двоичной системе счисления число 15 выглядит так:

13. Знаменитую игру “15” можно и поныне встретить в магазинах игрушек.

Пятнадцать утолщенных квадратиков с номерами от 1 до 15 находятся в квадратной коробочке. Цель игры состоит в том, чтобы, передвигая квадратики внутри коробочки, расположить их по порядку номеров.

Изобретение этой игры ошибочно приписывают Сэму Лойду. Однако идея создания этой головоломки принадлежит не ему. Лойд объявил, что создал свою головоломку в 1891 году, однако уже в 1877 году эта головоломка была запатентована Нойесом Чепменом, прототип которой он разработал в 1974 году.

14. В настоящее время (по состоянию на декабрь 2012 года) на территории России насчитывается 15 городов-миллионеров.

То есть городов, в которых население превышает миллион человек.

15. МАГИЧЕСКИЙ, или волшебный квадрат – это квадратная таблица, заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях постоянна.

В наименьшем магическом квадрате такой постоянной суммой

является число 15.

16. На циферблате часов со стрелками цифры 1 и 5 расположены на одной вертикали и симметрично относительно цифры 3.

Отметим при этом, что:

17. Великий композитор Дмитрий Дмитриевич ШОСТАКОВИЧ написал

18. КРАСОТА В 15 ТОЧКАХ

Возможно, вы видели подобное тому, что происходит на этой картинке.

Это удивительная способность нашего мозга видеть и распознавать движения человека. Ведь все, что есть на картинке – двигающиеся точки. Но мы видим не только человека и его движения, но и пол, сложение, эмоциональное состояние и даже некоторый характер.

И всю эту невероятно богатую информацию мы извлекаем из

15 движущихся точек

Источник: http://mindware.ru/blog/?p=3683

19. В следующих двух словах в совокупности 15 букв.

В программу Зимних Олимпийских игр входит 15 видов спорта.

20. Число 15 очень симметрично окружено с обеих сторон ПРОСТЫМИ числами.

21. Часто на циферблате часов расположено всего четыре числа. Эти числа можно разбить на две пары так, что сумма чисел в каждой паре будет равна 15.

22. На число 15 делятся без остатка следующие “ЭКЗОТИЧЕСКИЕ” числа:

А, следовательно, и такое:

А также и такое:

23. В тригонометрии чаще других чисел употребляются следующие:

НАИБОЛЬШИМ ОБЩИМ ДЕЛИТЕЛЕМ всех этих чисел является число 15.

24. В этих двух словах в совокупности 15 букв

В связи с этим предлагаем распутать следующий арифметический ребус.

Показать решение

   

25. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ была создана Альбертом Эйнштейном в 1905 году.

Отметим, в связи с этим, три любопытных факта.

• Число 1905 делится без остатка на 15.

• Сумма цифр числа 1905 равна 15.

• В следующем слове 15 букв:

26. Перед вами цепочка ЧИСЕЛ-ПАЛИНДРОМОВ и одновременно ЧИСЕЛ-ПЕРЕВЕРТЫШЕЙ, каждое из которых делится на 15.

27. А вот еще одна цепочка ЧИСЕЛ-ПАЛИНДРОМОВ и одновременно ЧИСЕЛ-ПЕРЕВЕРТЫШЕЙ, каждое из которых делится на 15.

28. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК ВНУТРИ КВАДРАТА.
Внутри квадрата на одной из его сторон построен равнобедренный треугольник с углами при основании по 15. Вершину третьего угла соединили с двумя вершинами противоположной стороны квадрата.

Докажите, что при этом образуется РАВНОСТОРОННИЙ треугольник (голубой треугольник на приведенном рисунке).

29. Синус 15 и косинус 15 являются, как известно, числами иррациональными, а их произведение является числом рациональным:

Аналогичным свойством обладает число 45:

Действительно, синус 45 и косинус 45 являются числами иррациональными, а их произведение — рациональное число:

30. Обычная шнуровка на кедах представляет собой некую ТОПОЛОГИЧЕСКУЮ задачу. Иногда — совсем непростую.

В Интернете приводится ровно 15 таких способов шнуровки. Вот некоторые из них:

31. На пульте телефона цифры от 1 до 9 расположены обычно так:

При этом

• сумма любых трех чисел, расположенных на прямой (по горизонтали, вертикали иди диагонали), проходящей через центральную клетку, равна 15;

• произведение любых трех чисел, расположенных не на вертикальной прямой, проходящей через центральную клетку, делится на 15.

32. Если в каком-нибудь месяце календарь выглядит так, как на этой табличке, то

• произведение всех чисел в каждой строке делится на 15;

• произведение всех чисел в каждом столбце, кроме одного, делится на 15.

33. ПЯТНАДЦАТЬ ФАНТАСТИЧЕСКИХ ФАКТОВ ОБ УЛЫБКЕ

Наверняка каждый из нас уже в курсе того, что приподнятое настроение и улыбка на лице способны продлить нам жизнь. Когда-то слышала такое утверждение, что полчаса смеха заменяет один стакан сметаны. Видимо, исключительно полезными свойствами.

В интернете собрано ровно 15 фактов несомненной и абсолютной пользы улыбок. Знакомьтесь.

(1) Даже улыбка через силу способна поднять вам настроение.

Психологи утверждают, что, заставляя себя улыбаться, любой человек может поднять себе настроение.

(2) Улыбка укрепляет иммунную систему.

Да-да, улыбка способна укрепить не только психическое, но и физическое здоровье человека, поскольку, когда мы улыбаемся, наше тело становится более расслабленным, что очень полезно для всего организма в целом.

(3) Улыбка заразительна.

Если кто-то недалеко от вас зевает, вам тоже невольно хочется зевнуть; если кто-то рядом с вами улыбается, вам тоже хочется улыбаться. Это не просто наблюдение – это вывод, сделанный учеными из Швеции.

(4) Улыбка уменьшает стресс.

Ну, конечно же! Что можно противопоставить стрессу? Только наши оптимизм и веру в светлое будущее. Если мы будем смеяться горестям в лицо, они неизбежно отступят.

(5) Легче улыбаться, чем хмуриться.

Для того чтобы нахмуриться, нам приходиться задействовать большее количество мышц, чем во время улыбки. Соответственно, на плохое настроение мы тратим гораздо больше энергии, чем на хорошее.

(6) Улыбка – универсальный знак счастья.

При знакомстве, во время комплиментов мы улыбаемся, потому что чувствуем себя чуточку счастливее и для того, чтобы показать окружающим свое к ним расположение. У всех народов улыбка – это знак хорошего настроения и позитивного настроя.

(7) На работе мы улыбаемся меньше.

В настоящее время на работе мы улыбаемся меньше, чем дома (28% против 30%). Это печально, не правда ли? Кстати, из этой ситуации имеется отличный выход – работа на дому Тольятти с возможностью улыбаться хоть в течение целого дня, при этом не выходя из дому.

(8) При улыбке работают от 5-ти до 53-х лицевых мышц.

Чем больше мышц работают, тем полезнее.

(9) Дети рождаются с умением улыбаться.

Каждый ребенок приходит в этот мир, уже умея улыбаться. По крайней мере, так заявляют ученые.

(10) Улыбка помогает нам получать повышение по службе.

«Улыбайся! Шеф любит идиотов!» Эта поговорка довольно грубо, однако очень точно определяет пользу улыбки в процессе продвижения карьеры.

(11) Улыбка – самое узнаваемое выражение лица.

В наш век (благодаря США) высоких технологий и (благодаря Японии) развивающейся семимильными шагами робототехнике, когда андроидов учат общаться с живыми людьми, а автоматы с мороженым выдавать мороженое только после широкой улыбки в камеру, распознание улыбки есть весьма полезное качество. Так вот именно ее на человеческом лице «диагностировать» проще и легче всего.

(12) Женщины улыбаются чаще мужчин.

Без комментариев. Разве что один: мы смотрим больше фильмов и много больше общаемся друг с другом на житейские темы.

(13) Улыбка более привлекательна, чем отличный макияж.

В ходе исследования было установлено, что 69% мужчин нашли привлекательными именно тех женщин, кто улыбался, а не тех, на ком лежал макияж от модного стилиста.

(14) Существуют 19 различных типов улыбок.

Сотрудники научной лаборатории в Сан-Франциско идентифицировали 19 разных типов улыбок и определили их в две категории – вежливые «социальные» улыбки, на которые требуется менее всего усилий, и искренние улыбки от души, каким нужно задействовать все 53 лицевые мышцы.

(15) Новорожденные сразу начинают улыбаться.

Большинство врачей уверены, что дети начинают улыбаться лишь в возрасте 4-6-ти недель, однако улыбки на лицах малышей появляются гораздо раньше – во время сна уже в первый день рождения. И когда вы увидите таким свое собственное чадо, попробуйте тогда сказать, что его улыбка – лишь невольное сокращение мышц, не получится.

34. Существует такая детская загадка.

Вот ответ на эту загадку:

На Солнце имеются ПЯТНА.
И в числе ПЯТНАДЦАТЬ содержатся “ПЯТНА”.

35. В следующих двух словах в совокупности имеется 15 букв.

На чертеже, который иллюстрирует теорему Пифагора, присутствуют 3 квадрата и 12 отрезков.

36. В дополнение к предыдущему пункту отметим, что и в следующих двух словах в совокупности имеется 15 букв.

В связи с этим, распутайте такой арифметический ребус, имеющий единственное решение.

Показать решение

   

37. КАЖДЫЙ ГОД ПУБЛИКУЮТ 15 НЕОБЫЧНЫХ МИРОВЫХ РЕКОРДОВ УХОДЯЩЕГО ГОДА

Вот некоторые из этих 15 рекордов за 2012 год.

• Лаша Патарая тянет 8,28 тонный грузовик левым ухом. Так он пытается попасть в книгу рекордов Гиннеса, 29 ноября, город Рустави, Грузия.

• Китайская компания по производству игрушек Mattel построила игрушечную железную дорогу, в шесть раз превосходящую по длине высоту шанхайской телебашни, одного из самых высоких зданий в мире. Длина рекордной дороги составила 2,888 километра.

• Художник Фан Янг, экспериментирующий с мыльными пузырями, установил мировой рекорд, поместив 181 человека внутри гигантского мыльного пузыря.

• Кеничи Ито, известный, как самый быстрый бегун на четырех конечностях, устанавливает в Токио мировой рекорд на стометровке, а именно 17,47 секунд.

• В Лондоне, 8 ноября, в одну машину класса мини забрались 28 женщин. Безусловный мировой рекорд в этой категории.

38. Это масштабное выступление проходило в северо-восточном индийском штате Ассам в присутствии представителей Книги рекордов Гиннеса.

15 ТЫСЯЧ БАРАБАНЩИКОВ, одетые в белые национальные костюмы, исполняли традиционную музыку на барабанах мриданга.

15 МИНУТ слаженной игры, и вот ансамбль признан рекордсменом по числу исполнителей.

39. В КНИГЕ РЕКОРДОВ ГИННЕСА ИМЕЮТСЯ 15 ДОМАШНИХ ЖИВОТНЫХ.

Вот некоторые из них.

• БОЛЬШЕ ВСЕГО ТЕННИСНЫХ МЯЧЕЙ ВО РТУ.

Собаки с удовольствием бегают за теннисными мячами, но вряд ли какой-либо пес любит заниматься этим больше, чем Ауги, 8-летний золотистый ретривер, установивший мировой рекорд за наибольшее разовое количество теннисных мячей в пасти. Ауги успешно собрала и держала пять мячей.

• САМАЯ ВЫСОКАЯ СОБАКА.

Гигант Джордж, дог высотой 110 см в холке и 2 метра и 21 сантиметр от носа до хвоста из г.Тусон, штат Аризона, США, обладает двумя мировыми рекордами: самая высокая живущая собака и самая высокая собака в истории.

• ЛОПАНИЕ ШАРИКОВ.

Лопание 100 надувных шариков за 44,49 секунд было лишь началом славы Анастасии. Анастасия живет в Лос-Анджелесе со своей хозяйкой и тренером Дори Ситтерли.

• САМЫЙ ВЫСОКИЙ КОТ.

Кошка породы Саванна по имени Мэджик получила звание самого высокого домашнего кота, ее рост составляет 43,4 см от холки до лап.

• БАЛАНСИРОВАНИЕ СТАКАНА ВОДЫ.
Свит Пи обладает парой самых странных рекордов: наибольшее количество шагов вперед и вниз, совершенных собакой, удерживающей 150-миллитровый стакан воды (10 шагов), и самая быстрая стометровка в исполнении собаки с жестяной банкой на голове (2 минуты и 55 секунд).

• НАИБОЛЬШЕЕ КОЛИЧЕСТВО СОБАК, ПРЫГАЮЩИХ НА СКАКАЛКЕ.

“Собаки Учиды Гейнуши” – гвоздь программы японского Цирка Супер Ван Ван.

13 “артистов” цирка заслужили мировой рекорд за наибольшее количество собак, прыгающих на скакалке.

40. РЕКОРД, УМНОЖЕННЫЙ НА 15.

Чтобы выявить истинную продуктивность растений, их надо освободить от «власти земли», писал Тимирязев. По этому пути идут исследователи, разрабатывающие методы выращивания растений без почвы.

Но еще больших результатов можно добиться, если освободить растения от власти Солнца, точнее, от заданного природой чередования светлого и темного времени суток, короткого и длинного дня и т. д.

Например, считается, что предельный урожай одного из самых продуктивных сортов пшеницы в поле может достигать 100 ц/га. Даже в идеальных условиях, на крохотных делянках, превзойти этот результат ни разу не удалось.

А в установках с непрерывным освещением за год получили с квадратного метра три урожая по 5 кг. В пересчете на гектар, это 1500 ц — в ПЯТНАДЦАТЬ раз больше полевого рекорда.

Такие же результаты получены и при выращивании помидоров.

41. Атомный номер ФОСФОРА в периодической таблице Менделеева – 15.
Пытаясь найти философский камень, немецкий алхимик Хенниг Бранд в 1669 году выделил фосфор.Название «фосфор» происходит от греческих слов «φῶς» — свет и «φέρω» — несу.

В следующих словах в совокупности 15 букв. Усовершенствованный способ получения фосфора, применяемый до сих пор, был опубликован в 1743 году Андреасом Маргграфом. В следующих двух словах в совокупности 15 букв.

Фосфор является важнейшим биогенным элементом и в то же время находит очень широкое применение в промышленности.

Красный фосфор применяют в производстве спичек. Его вместе с тонко измельчённым стеклом и клеем наносят на боковую поверхность коробки. При трении спичечной головки, в состав которой входят хлорат калия и сера, происходит воспламенение.

42. Существует способ, как при помощи одной-единственной спички поднять одновременно 15 спичек:

43. Очень популярна следующая головоломка со спичками.

При помощи 15 спичек изобразили корову, которая смотрит налево (на рисунке она смотрит на других коров – не спичечных) . Нужно переставить две спички так, чтобы получилась корова из спичек, которая смотрит в противоположную сторону – направо.

Показать решение

44. УДИВИТЕЛЬНЫЙ ТРЕУГОЛЬНИК

Оказывается, у этого треугольника имеется целый ряд очень любопытных свойств.
Вот лишь некоторые из них.

СВОЙСТВО 1. Гипотенуза15-ти градусного треугольника в 4 раза больше высоты, проведенной к этой гипотенузе.

СВОЙСТВО 2. Пусть вершины одного квадрата расположены на сторонах другого так, что каждый из выделенных на рисунке углов равен 15°. Тогда площадь наружного квадрата в 1.5 раза больше площади внутреннего квадрата.

СВОЙСТВО 3. Если внутри одного квадрата расположен другой квадрат так, что прямые содержащие стороны меньшего квадрата, проходят через вершины большего и образуют со сторонами наружного квадрата углы величиной 15°, то площадь наружного квадрата в 2 раза больше площади внутреннего квадрата.

СВОЙСТВО 4. Квадрат можно разбить на 15-ти градусные треугольники.

СВОЙСТВО 5. Правильный 12-ти угольник можно разбить на 15-ти градусные треугольники.

СВОЙСТВО 6. Если длины сторон прямоугольника являются рациональными числами, то его можно разбить на 15-ти градусные треугольники.

45. В этих двух словах в совокупности 15 букв.

46. ХОРОШИЕ ШУТКИ — юмористическая телевизионная программа на телеканале СТС.

Отметим, что в следующих двух словах в совокупности 15 букв.

Шоу представляет собой игру, построенную по принципу «юмористических боев без правил». Две команды соревнуются друг с другом в ряде шуточных конкурсов.

За каждый из конкурсов команды получают оценки жюри, складывающиеся из голосования 15 зрителей из зала.

47. Из цифр числа 15 можно составить следующую цепочку любопытных равенств. В правой части каждого из равенств находится число, которое начинается цифрой 1, а оканчивается цифрой 5.

48. В следующих двух словах в совокупности 15 букв.

• Великий русский композитор Николай Андреевич РИМСКИЙ –КОРСАКОВ сочинил 15 опер.

• Мемориальный музей-квартира Римского-Корсакова является единственным композиторским музеем Санкт-Петербурга. Здесь Римский-Корсаков прожил 15 лет.

Программа внеурочной деятельности по математике для обучающихся 5 класса «Головоломки»

Муниципальное автономное общеобразовательное учреждение

Заместитель директора по ВР Директор МАОУ СОШ №4

________________/Никонова И. Г./ Приказ №

В соответствии с ФГОС ООО внеурочная деятельность является обязательным компонентом содержания ООП ООО.

Математическое образование является обязательной и не­отъемлемой частью общего образования на всех ступенях школы. Оно играет важную роль как в практической, так и в духовной жизни общества. В школе математика служит опорным предметом для изучения смежных дисцип­лин, поэтому необходимо сформировать систему внеурочной деятельности по математике, цели и задачи которой должны сочетаться с основными целями и задачами обучения математике.

На основе этого можно выделить основные цели внеурочной деятельности по математике:

– развитие и углубление знаний по программному материалу;

– интеграция и практическое применение математики.

Внеурочная деятельность по математике направлена на углубление знаний учащихся в области программного материала, развитие их логического мышления, воображения, развитие у обучающихся мотивации к познанию и творчеству, содействие личностному самоопределению, их адаптации к жизни в обществе.

Цель курса внеурочной деятельности «Головоломки»: оказание помощи в освоении ООП и развитии детям с особыми образовательными потребностями, в частности, школьникам с высоким уровнем обучаемости.

Задачи курса внеурочной деятельности «Головоломки»:

1. Пробуждение и развитие устойчивого интереса к математике.

2. Расширение и углубление знаний по программному материалу

3. Расширение и углубление представлений учащихся о практическом значении математики в жизни общества.

4. Установление более тесных деловых контактов между учителем математики и обучающимися и на этой основе более глубокое изучение познавательных интересов и запросов школьников.

5. Развитие способностей по самостоятельному приобретению знаний, умений, навыков школьниками, ускорению процесса перехода от обучения к самообучению – наивысшей ступени образовательного процесса.

6. Создание актива обучающихся, способного добиться высоких результатов при участии в конкурсах и олимпиадах на школьном, муниципальном, всероссийском и международном уровнях.

Реализация поставленной цели и обозначенных задач частично осуществляется на уроках. Однако в процессе классных занятий, ограниченных рамками учебного времени и программы, это не удается сделать с достаточной полнотой. Поэтому окончательная и полная реализация этих целей переносится на внеурочные занятия.

Вместе с тем между учебно-воспитательной работой, проводимой на уроках, и внеклассной работой существует тесная взаимосвязь: учебные занятия, развивая у учащихся интерес к знаниям, содействуют развертыванию внеклассной работы, и, наоборот, внеклассные занятия, позволяющие учащимся применить знания на практике, расширяющие и углубляющие эти знания, повышают успеваемость учащихся и их интерес к учению.

Решение задач занимает в математическом образовании огромное место. Значительная часть обучающихся испытывает серьёзные затруднения при решении текстовых задач, в особенности задач повышенной сложности и олимпиадных заданий. В большей степени это связано с недостаточной сформированностью у обучающихся умения составлять план действий, алгоритм решения конкретной задачи, культурой моделирования явлений и процессов. Большинство обучающихся решают такие задачи лишь на репродуктивном уровне. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Их решение способствует экономическому образованию обучающихся, развитию логического мышления, сообразительности и наблюдательности.

В основе курса лежат следующие нормативные документы и примерные программы:

Федеральный закон от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» (редакция от 23.07.2013);

Основная образовательная программа Основного общего образования от 08.04.15;

Основная образовательная программа МАОУ СОШ №4;

Учебный план школы на 2016-2017 учебный год.

Предлагаемый курс внеурочной деятельности «Головоломки» демонстрирует обучающимся применение математического аппарата к решению как повседневных бытовых проблем каждого человека, так и к решению задач повышенной сложности и олимпиадных задач. Познавательный материал курса будет способствовать формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также познавательной и социальной активности.

Программа внеурочной деятельности «Головоломки» адресована учащимся 5 классов. Данный курс рассчитан на 35 часов, предполагает решение различных головоломок и олимпиадных заданий, а также математических задач, связанных с окружающей нас жизнью.

Занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изученном материале, на решение новых и интересных задач.

У обучающихся могут быть сформированы личностные результаты:

ответственное отношение к учению, готовность и способность обучающихся к самообразованию на основе мотивации к обучению и познанию, осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учётом устойчивых познавательных интересов;

способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

умение контролировать процесс и результат математической деятельности;

коммуникативная компетентность в общении и сотрудничестве со сверстниками в образовательной, учебно-исследовательской, творческой и других видах деятельности;

критичность и креативность мышления, инициативы, находчивости, активности при решении задач.

составлять план и последовательность действий;

определять последовательность промежуточных целей и соответствующих им действий с учётом конечного результата;

предвидеть возможность получения конкретного результата при решении задач;

осуществлять констатирующий и прогнозирующий контроль по результату и способу действия;

концентрировать волю для преодоления интеллектуальных затруднений и физических препятствий;

адекватно оценивать правильность и ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения.

устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;

видеть математическую задачу в других дисциплинах, окружающей жизни;

выдвигать гипотезу при решении учебных задач и понимать необходимость их проверки;

планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

выбирать наиболее эффективные и рациональные способы решения задач;

интерпретировать и оценивать информацию (критическая оценка, оценка достоверности).

организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников;

взаимодействовать и находить общие способы работы; работать в группе; находить общее решение и разрешать конфликты на основе согласования позиции и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

прогнозировать возникновение конфликтов при наличии различных точек зрения;

координировать и принимать различные позиции во взаимодействии;

аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности.

самостоятельно приобретать и применять знания в различных ситуациях для решения различной сложности практических задач;

уметь решать задачи с помощью перебора возможных вариантов;

выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;

применять изученные понятия, результаты и методы при решении задач из различных реальных ситуаций, не сводящихся к непосредственному применению известных алгоритмов;

самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем, а также самостоятельно интерпретировать результаты решения задачи с учётом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

– Федеральный государственный образовательный стандарт основного общего образования. – М.: Просвещение, 2014.

– Цветкова М. С. Информатика. Математика. Программы внеурочной деятельности для основной школы: 3 – 6 классы. / М. С. Цветкова, О. Б. Богомолова, Н. Н. Самылкина. – М.: БИНОМ. Лаборатория знаний, 2015.

– Математика. 5–6 классы. Организация познавательной деятельности / авт.-сост. Г. М. Киселева. – Волгоград: Учитель, 2015.

Попова Л.П. Сборник практических задач по математике: 5 класс

Выговская В.В. Сборник практических задач по математике: 6 класс.

Шевкин А. В. Текстовые задачи по математике. 5 – 6 классы.

Аленков Ю. – 650 головоломок и задач на сообразительность

Байиф Ж-К. – Логические задачи

Барр С. – Россыпи головоломок

Белов Н. – Занимательные головоломки

Бизам Д. , Герцер Я. – Игра и логика. 85 логических задач

Бизам Д., Герцер Я. – Многоцветная логика. 175 логических задач

Брехер Э. – Нестандартные логические головоломки

Быльцов С. – Логические головоломки и задачи. Занимательная математика для всей семьи

Быльцов С. – Математические игры, пасьянсы и фокусы. Занимательная математика для всей семьи

Вуджек Т. – Тренировка ума

Гайштут А. – Математика в логичесих упражнениях

Гамов Г., Стерн М. – Занимательная математика

Гарднер М. – 1000 развивающих головоломок

Гарднер М. – Математические головоломки и развлечения

Гершензон М. – Головоломки профессора Головоломки

Дженкинс Д., Биар М. – Математические головоломки

Диксон К. – Увлекательные головоломки для умных

Докучаева Н. – Головоломки своими руками

Доморяд А. – Математические игры и развлечения

Дьюдени Г. – 200 знаменитых головоломок мира

Дьюдени Г. – 520 головоломок

Кириченко И. – Головоломки для детей и взрослых

Кордемский Б. – Математические завлекалки

Кордемский Н., Русалев Н. – Удивительный квадрат

Куликов А. – Задачи, Ребусы, Головоломки стран мира

Куликов А. – Лучшие логические игры и головоломки

Мочалов Л. – Головоломки и занимательные задачи

Перельман Я. – Занимательная математика

Рассел К., Картер Ф. – Математические задачи на логику, смекалку и воображение

Ржевский С. – Математические развлечения

Савин А. – Занимательные математические задачи

Слоун П., МакХейл Д. – Оригинальные головоломки

Сухин И. – 800 новых логических и математических головоломок

Таунсенд Ч. – Самые веселые головоломки

Харт-Дэвис А. – Удивительные математические головоломки

Шапиро С. – Решение логических и игровых задач

Шарыгин И., Шевкин А. – Математика. Задачи на смекалку

ОБРАЗЦЫ КАРТОЧЕК ДЛЯ ОРГАНИЗАЦИИ РАБОТЫ
НА ЗАНЯТИЯХ ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ

ЗАДАЧИ С ЧИСЛАМИ

1. Найти наименьшее число, которое обладает сле­дующими свойствами:

если вычесть из него 1, оно делится (без остат­ка) на 9

если вычесть из него 2, оно делится (без остат­ка) на 8

если вычесть из него 3, оно делится (без остат­ка) на 7

если вычесть из него 4, оно делится (без остат­ка) на 6

если вычесть из него 5, оно делится (без остат­ка) на 5

если вычесть из него 6, оно делится (без остат­ка) на 4

если вычесть из него 7, оно делится (без остат­ка) на 3

если вычесть из него 8, оно делится (без остат­ка) на 2.

2. В числе 64517 зачеркните одну цифру так, чтобы полученное число было наибольшим из всех возможных.

3. В числе 425387 зачеркните две цифры так, чтобы полученное число было наименьшим из всех возможных.

4. В числе 34517 зачеркните одну цифру так, чтобы полученное число было наименьшим из всех возможных.

5. В числе 6274317 зачеркните три цифры так, чтобы полученное число было наибольшим из всех возможных.

6. Вычеркни в числе 5010671 пять цифр так, чтобы оставшееся число было наибольшим.

7. Вычеркните в числе 400538 пять цифр так, чтобы оставшееся число было наибольшим.

8. Записаны три числа: 111, 777, 999. Надо зачеркнуть шесть цифр так, чтобы оставшиеся числа составляли вместе 20?

9. На доске написано число: 1234567891011121314151617181920.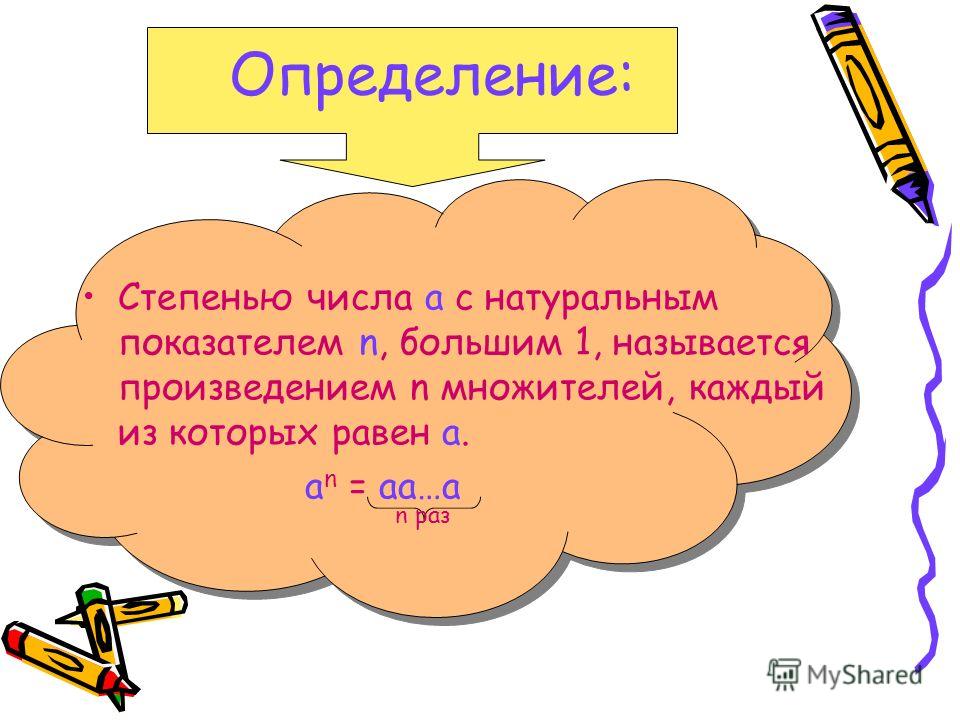 Из этого числа нужно вычеркнуть 21 цифру таким образом, чтобы оставшееся число было наибольшим.

10. Из числа 123456789101112…57585960 вычеркните 100 цифр так, чтобы оставшееся число было наибольшим.

11. В стозначном числе 12345678901234567890… 1234567890 вычеркнули все цифры, стоящие на нечетных местах. В полученном пятидесятизначном числе вновь вычеркнули все цифры на нечетных местах. Вычеркивание про­должается до тех пор, пока не останется одна цифра. Какая это цифра?

12. Расшифруйте комбинацию кодового замка, если:

1) третья цифра на 3 больше, чем первая.

2) вторая цифра на два больше, чем четвёртая.

3) в сумме все цифры дают число 17.

4) вторая цифра 3.

13. Из цифр 1, 2, 3, 4 составлены четырехзначные числа так, что цифры в записи числа не повторяются. В ответе запишите разность между наибольшим и наименьшим из полученных чисел.

14. Сумма пяти последовательных чисел равна чис­лу 1989. Найдите эти числа.

15. Сумма цифр двузначного числа равна наибольшему однозначному числу, а число десятков на три меньше этой суммы. Найдите это число.

16. Одно из трех слагаемых есть наибольшее трехзначное число, другое слагаемое равно разности между наименьшим четырехзначным числом и наибольшим двузначным числом. Чему равно третье слагаемое, если сумма всех трех слагаемых равно 3276?

17. Найдите наименьшее число, которое делится без остатка на следующие 9 чисел: 2, 3, 4, 5, 6, 7, 8, 9 и 10.

18. Представьте число 231 в виде суммы нескольких натуральных чисел так, чтобы произведение эти слагаемых тоже равнялось 231.

19. Сколько различных произведений, кратных десяти, можно образовать из чисел 2, 3, 5, 7, 9?

20. Сколько всего можно составить четырехзначных чисел, сумма которых равна трем. Запиши все эти числа.

21. Сколько произведений, кратных десяти, можно образовать из чисел 2, 3, 5, 5, 7, 9?

22. Какую цифру X нужно приписать к числу 97 справа и слева, чтобы полученное число Х97Х делилось на 27?

23. Если написать последовательно все числа от 1 до 1000, то мы получим ряд из 1000 чисел. Если же теперь сложить все числа такого ряда, то их сумма выразится любопытным числом. Какова же будет эта сумма?

Каким способом можно быстро подсчитать суммы чисел от 1 до 100 и до 1000?

24. Если написать последовательно все числа от 1 до 1000, то сколько раз в таком ряду чисел встретится цифра 3?

25. Взгляните на этот ряд чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Можете ли вы сразу сказать, что больше – их сумма или произведение?

26. Какой цифрой оканчивается произведение:

а) всех натуральных чисел от 11 до 19;

б) всех нечетных натуральных чисел от 1 до 121;

в) 3 · 13 · 23 · 33 · 43 · 53 · 63 · 73 · 83 · 93?

27. Сколько нулей стоит в конце произведения всех натуральных чисел от 10 до 25?

28. Какой цифрой оканчивается произведение любых пяти последовательных натуральных чисел?

29. Произведение нескольких последовательных нечетных натуральных чи­сел оканчивается цифрой 7. Сколько в этом произведении множителей?

30. Произведение каких двух целых чисел всегда меньше их суммы?

31. Произведение каких трех целых чисел равно их сумме?

32. Цифра десятков у двузначного числа в два раза меньше цифры единиц. Если эти цифры переставить, то получится число, большее первоначального на 36. Найдите это число.

33. Если приписать цифру 1 впереди некоего 5-тизначного числа, то получится число в 3 раза меньше, чем если приписать цифру 1 в конце этого же числа. Найдите это число.

34. На доске было написано два одинаковых числа. Степа приписал к одному из них впереди 100, а ко второму сзади 1. Оказалось, что первое число стало ровно в 37 раз больше второго. Какие числа были написаны на доске?

35. Цифру 9, с которой начиналось трехзначное число, перенесли в конец числа. В результате получилось число на 216 меньшее. Какое число было первоначально?

36. Трёхзначное число начинается с цифры 7. Из него получили другое трехзначное число, переставив эту цифру в конец числа. Полученное число оказалось на 117 меньше предыдущего. Какое число получилось?

37. Некоторое трёхзначное число состоит из различных цифр, следующих в порядке возрастания, а в его названии все слова начинаются с одной и той же буквы. Другое трехзначное число, наоборот, состоит из одинаковых цифр, но в его названии все слова начинаются с разных букв. Найдите эти числа.

38. Задумано трехзначное число, у которого с любым из чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?

39. Переставь цифры в квадратах так, чтобы две следующие друг за другом не оказались в соседних клетках – ни по вертикали, ни по горизонтали, ни по диагонали.

40. Разделите сетку на прямоугольные и квадратные блоки таким образом, чтобы каждый блок содержал только одно число, равное количеству клеток в этом блоке.

																4
				16								4				12	8				2
	4				10								3					15
								24
8					18											16
													6
			12									24								6
			4
2	2

41. В таблице, состоящей из шести строк и шести столбцов, «спрятались» пять кораблей, которые нужно найти. Это один корабль длиной 4 клетки, один корабль длиной 3 клетки, два корабля длиной две клетки и два корабля длиной одна клетка. Числа снизу и справа показывают количество занятых кораблями клеток в соответствующей строке или столбце. Расставьте корабли в таблице. Примечание: корабли не могут соприкасаться.

					4									3
					1									1
					0									2
					1									3
					3									3
2	1	3	0	3										1
								2	2	0	5	0	4

РАССТАВЬТЕ ЗНАКИ И СКОБКИ

1. Расставьте скобки и знаки арифметических действий так, чтобы получить указанные числа:

5 5 5 5 = 3 5 5 5 5 = 4 5 5 5 5 = 5 5 5 5 5 = 6

5 5 5 5 = 7 5 5 5 5 = 26 5 5 5 5 = 30 5 5 5 5 = 50

5 5 5 5 = 55 5 5 5 5 = 120 5 5 5 5 = 130 5 5 5 5 = 625

2. В записи 5 5 5 5 поставьте между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно:

а) 20; б) 110; в) 560.

3. Используя три цифры 5, знаки арифметических действий и скобки, составьте несколько выражений, имеющих различные значения.

4. В записи 5 5 5 5 5 5 = 615 расставьте знаки сложения так, чтобы получилось верное равенство.

5. Поставьте между цифрами знаки арифметических действий и скобки так, чтобы в результате получилось по 1. Две рядом стоящие цифры можно считать двузначным числом.

1 2 3 = 1
1 2 3 4 = 1
1 2 3 4 5 = 1
1 2 3 4 5 6 = 1
1 2 3 4 5 6 7 = 1
1 2 3 4 5 6 7 8 = 1
1 2 3 4 5 6 7 8 9 = 1

 

6. Расставьте знаки сложения, вычитания, умно­жения и деления так, чтобы ответы во всех стро­ках были правильными. Разрешается использовать скобки.

1 2 = 3

1 2 3 = 4
1 2 3 4 = 5
1 2 3 4 5 = 6
1 2 3 4 5 6 = 7
1 2 3 4 5 6 7 = 8
1 2 3 4 5 6 7 8 = 9
1 2 3 4 5 6 7 8 9 = 10

 

7. Употребляя цифру 7 по 4 раза, знаки действий и скобки, представьте все числа от 1 до 10 включительно.

8. Расставьте между цифрами знаки четырёх действий и скобки разными способами так, чтобы результат вычислений составлял 100.

1 2 3 4 5 6 7 8 9 = 100

1 2 3 4 5 6 7 8 9 = 100
1 2 3 4 5 6 7 8 9 = 100

1 2 3 4 5 6 7 8 9 = 100

9. В записи 9 9 9 9 9 9 9 9 поставьте знаки сложения и вычитания так, чтобы значение получившегося выраже­ния было равно 1998.

10. Расставьте знаки сложения между цифрами 1 2 3 4 5 6 7 так, чтобы в сумме получилось число 100.

11. В записи 6 6 6 6 6 6 6 6 поставьте между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно:

а) 264; 6) 13332; в) 67332.

Найдите еще 5 ответов, которые можно получить, ставя знак «+» между некоторыми цифрами в записи 6 6 6 6 6 6 6 6.

12. Применяя знаки сложения, можно восемью восьмерками записать число 1000:

888 + 88 + 8 + 8 + 8.

Используя знаки арифметических действий и скобки, запишите число 1000 восемью восьмерками другим способом.

13. Применяя знаки арифметических действий и скобки, запишите:

а) семью семерками 700; г) десятью четверками 500;

б) восемью семерками 700; д) десятью шестерками 600;

в) восемью двойками 200; е) десятью девятками 1000.

14. Между цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 расставьте знаки арифметических действий и скобки так, чтобы полученное выражение имело значение 100.

15. Из четырех двоек составьте выражения, значения которых равнялись бы числам: 0, 1,2, 3, 4, 5, 6, 8, 9, 10.

16. Расставьте знаки и скобки так, чтобы получились верные равенства:

9 9 9 = 2

9 9 9 = 10

9 9 9 = 90

9 9 9 = 9

17. Применяя все четыре арифметических действия и скобки, напишите четырьмя тройками порядковые числа от 1 до 10.

18. Как можно написать число 100:

а) пятью единицами, г) семью шестерками,

б) пятью тройками, д) шестью семерками?

в) пятью пятерками,

19. Найдите все натуральные числа, которые можно записать четырьмя единица­ми, употребляя только знаки сложения или вычитания.

20. Расставьте знаки сложения или вычитания между цифрами

1 2 3 4 5 6 7 так, чтобы в результате получилось число 55.

21. Вставьте пропущенные знаки действий « + » или « – », чтобы получилось верное равенство:

а) 5 4 3 2 1 = 3 б) 5 4 3 2 1 = 5

22. Расставьте знаки арифметических действий и, если нужно, скобки так, чтобы получилось верное равенство: 1 2 3 4 5 6 7 8 = 9

23. Расставь знаки арифметических действий и если нужно скобки так чтобы получились верные равенства

7 7 7 7 = 15

7 7 7 7 = 8

7 7 7 7 = 294

24. В записи 1 * 2 * 3 * 4 * 5= 100 замените каждую из звездочек знаками арифметических действий и расставьте скобки так, чтобы получилось верное равенство.

25. Запишите число 1000 шестью тройками, используя знаки арифметических действий.

26. Используя знаки арифметических действий и скобки, запишите число 100: а) пятью пятерками; б) четырьмя пятерками.

27. Поставьте знаки сложения и вычитания между цифрами

9 8 7 6 5 4 3 2 1

так, чтобы значение получившегося выражения было равно 100.

28. Применяя знаки арифметических действий, запишите тремя двойками числа: а) 1; б) 2; в) 3.

29. Четырьмя двойками с помощью знаков арифметических действий запишите выражения, значения которых равны:

а) 1; б) 2; в) 3; г) 4; д) 5; е) 6; ж) 8; з) 9; и) 10.

30. Применяя знаки арифметических действий и скобки, запишите число 200: а) 5; б) 7; в) 8; г) 9 двойками.

31. Применяя знаки арифметических действий и скобки, запишите четырьмя семерками числа:

а) 1; б) 2; в) 3; г) 4; д) 5; е) 6; ж) 7; з) 8; и) 9; к) 10.

32. В примере 9 * 7 * 3 * 5 * 2 = 10 поставьте вместо каждой из звездочек знаки сложения или вычитания так, чтобы равенство было верным.

33. Выразить число 100 шестью одинаковыми цифрами, используя для этого только знаки арифметических действий и скобки.

34. Запишите число 100 с помощью цифр 1, 2, 3, 4, 5, не изменяя их порядка, пользуясь для этого только знаками арифметических действий и скобками.

35. Запишите ноль тремя пятёрками, используя для этого только знаки арифметических действий и скобки.

36. Запишите число пять тремя пятёрками, используя для этого только знаки арифметических действий и скобки.

37. Изобразите число 31 шестью тройками. Пятью тройками.

38. Выразите число 1000 шестью пятёрками, используя для этого только знаки математических действий и скобки.

39. Поставь знаки действий и, если нужно, скобки так, чтобы получились верные равенства:

3 3 3 3 3 = 198 3 3 3 3 3 = 72 3 3 3 3 3 = 366

3 3 3 3 3 = 243 3 3 3 3 3 = 22 3 3 3 3 3 = 0

3 3 3 3 3 = 37

40. Расставьте знаки арифметических действий и скобки так, чтобы получились верные равенства
 

4 4 4 4 = 1 4 4 4 4 = 2 4 4 4 4 = 3 4 4 4 4 = 4

4 4 4 4 = 5 4 4 4 4 = 6 4 4 4 4 = 7 4 4 4 4 = 8

4 4 4 4 = 9 4 4 4 4 = 10

41. Расставьте знаки «плюс» между цифрами числа 987 654 321 таким образом, чтобы в сумме получилось 99.

42. Расставьте в левой части равенства скобки и знаки арифметических действий так, чтобы выполнилось равенство:

а) 7 7 7 7 7 7 7 7 = 700

б) 6 6 6 6 6 6 6 6 6 = 600

в) 4 4 4 4 4 4 4 4 4 4 = 500

ЧИСЛОВЫЕ РЕБУСЫ 1

1. Поставьте вместо звездочки цифры так, чтобы получилось верное равенство:

1) ** + ** = 197

2) 4* + **2 = **01

3) *3 · 3* = 3**

4) *** – ** = 1

5) 91 · ** = ***

6) **1 · 9 = ***

7) ** · * – * = 1

2. Существуют ли такие цифры, обозначенные звездочками, что:

*** + *** = *999

3. Сколько всего решений имеет задача? Восстановите запись:

*** · 9 = ***

4. Расшифруйте запись ** + *** = ****, если известно, что оба слагаемых и сумма не изменятся, если прочитать их справа налево.

5. Восстановите запись:

6. В поврежденной рукописи в числовом примере удалось разобрать только одну цифру и два знака арифметических действий, остальные, неразличимые, циф­ры обозначены звездочками:

Восстановите пример полностью.

7. Восстановите запись:

8. Найдите неизвестные цифры в записи:

9. Восстановите записи:

10. В примере на умножение

допущена ошибка. Откуда это видно?

11. Восстановите запись:

12. Восстановите запись:

13. На какое наименьшее натуральное число нужно умножить число 7 для того, чтобы получить число, записывающееся одними девятками?

14. На какое наименьшее натуральное число нужно умножить число 333667 для того, чтобы получить число, записывающееся одними восьмерками?

15. На какое наименьшее натуральное число нужно умножить число 12345679 для того, чтобы получить число, состоящее из одних пятерок?

ЧИСЛОВЫЕ РЕБУСЫ 2

1. Расшифруйте запись. Одинаковым буквам соответствуют одинаковые цифры, а разным буквам соответствуют разные цифры.

А + АБ +АБВ = БВБ

2. Восстановите записи:

а) АВ · АВ = АСС

б) АА + АА = ВАС

3. Решите ребусы:

а) АВ · А = ССС;

б) А · В · АВ = ВВВ;

в) АА · АВС · ВС = АВСАВС.

4. Восстановите запись:

ДА · МА = ЯЯЯ.

5. Пусть дан числовой ребус:

Число 8126 является решением ребуса, так как при замене буквы У на цифру 8, буквы Д на 1, буквы А на 2, буквы Р на 6 получается верный пример на сложение.

Проверьте, является ли число 5621 решением числового ре­буса:

6. Решите числовые ребусы:

7. Вова любит решать числовые ребусы. Он сам составил три ребуса, но никак не может их решить. Объясните, по какой причине эти ребусы не имеют решения.

8. Решите ребус:

9. Ребус

не имеет решения. Почему?

11. Восстановите записи:

БИР + БИР + БИР + БИР = ДОРД

ЛИСА + ВОЛК = ЗВЕРИ

ДЕСЯТЬ : ДВА = ПЯТЬ

ДВА · ДВА = ЧЕТЫРЕ

 

12. Замените звездочки цифрами:

13. Одинаковым фигурам на рисунке соответствуют одинаковые цифры. Найдите эти цифры.

 

14. Если АБ · ВГ = ДДД, а Д · ВГ – АБ = ВВ, то чему равно произведение АБ · Г?

НАЙТИ ОШИБКУ В РАССУЖДЕНИЯХ

 

1. Найдите ошибку в каждом из примеров:

а) 225 : 25 + 75 = 100 – 16

25 (9 : 1 + 3) = 84

25 · 12 = 84

25 = 7 (?!) В чём ошибка?

б) 5005 – 2002 = 35 · 143 – 143 · 14

5005 – 35 · 143 = 2002 – 143 · 14

5 (1001 – 7 · 143) = 2 (1001 – 7 · 143)

5 = 2 (?!) В чём ошибка?

2. Возьмём числовое тождество:

35 + 10 – 45 = 42 + 12 – 54

5 · 7 + 5 · 2 – 5 · 9 = 6 · 7 + 6 · 2 – 6 · 9

5 (7 + 2 – 9) = 6 (7 + 2 – 9)

Разделим обе части на множитель (заключённый в скобки), получим:

5 = 6 (?!) В чём ошибка?

 

3. Возьмем очевидное равенство: 16 : 16 = 25 : 25.

После вынесения за скобки общего множителя из каждой части этого равенства будем иметь:

16 · (1 : 1) = 25 · (1 : 1)

Зная, что 1 : 1 = 1, получаем 4 · 4 = 25 (?!) В чём ошибка?

 

4. Найдите ошибку в математических выкладках:

x = 2

x (x – 1) = 2 (x – 1)

x2 – x = 2x – 2

x2 – 2x = x – 2

x (x – 2) = x – 2

x = 1 (?!) В чём ошибка?

5. а) Ученик переписал числовое выражение, значение которого равно 58, но забыл поставить скобки. У него получилось:

6 · 8 + 20 : 4 – 2.

Где в этом выражении должны стоять скобки?

б) Расставляя в том же выражении скобки разными способами, можно получить другие ответы. Какие?

6. Коля написал:

21 : 8 – 5 · 2 + 6 : 3 = 16.

Потом выяснилось, что он забыл поставить скобки. В каких местах?

7. В записи

9 · 6 + 14 : 2 + 2 : 3 + 7 = 22

расставьте две пары скобок так, чтобы получилось верное равенство.

8. Переместите одну любую четверку, чтобы равенство стало верным:

44 + 4 = 444 : 4 – 44 : 4 + 4 : 4

9. Расставьте скобки так чтобы получились верные равенства, сделайте проверку:

6 + 2 · 10 = 80

40 : 8 : 4 = 20

35 – 10 : 5 = 5

10. Расставь скобки, чтобы получились верные равенства:

7 · 8 + 4 : 4 + 2 = 17

7 · 8 + 4 : 4 + 2 = 10

7 · 8 + 4 : 4 + 2 = 65

7 · 8 + 4 : 4 + 2 = 77

11. Расставьте скобки, чтобы получились верные равенства:

а) 140 – 40 : 4 – 2 = 28

б) 1395 : 45 – 10 · 170 – 140 : 10 = 1

в) 360 – 270 : 9 + 6 · 3=350
г) 69 – 54 : 3 + 6 = 11

д) 15 – 35 + 5 : 4 = 5

е) 945 : 791 : 7 − 92 = 45

ж) 526 + 213 − 83 : 26 = 531

з) 78 – 43 · 285 : 15 = 665

и) 8 · 873 : 9 : 194 = 4

к) 104 – 99 · 66 : 15 = 22

л) 585 : 34 + 542 − 537 = 15

м) 804 – 920 : 184 · 42 = 594

н) 55 · 12 : 422 − 392 = 22

о) 999 – 852 · 5 + 249 = 984

п) 495 + 15 : 455 − 425 = 17

р) 538 + 281 + 103 + 33 = 955

с) 963 − 640 + 477 + 46 = 846

т) 10 · 83 – 154 · 2 = 522

у) 198 : 66 · 270 : 9 = 90

ф) 131 · 7 – 666 · 3 = 753

х) 136 − 72 − 620 : 155 = 60

ц) 3 · 323 − 954 − 368 = 383

ч) 101 · 2 + 59 − 46 = 215

ш) 115 − 21 − 969 : 57 = 111

щ) 81 · 7 : 351 : 13 = 21

ъ) 796 + 147 − 143 − 240 = 560

ы) 364 : 91 · 50 + 289 = 489

ь) 289 – 284 · 55 − 26 = 145

э) 311 + 278 − 324 − 133 = 398

ю) 370 − 293 : 73 − 66 = 11

12. Вместо «?» поставить знаки арифметических действий, так чтобы получились верные равенства:

а) 780 ? 46 ? 2 = 872

б) (18 ? 17) ? 18 = 17

в) 4 ? 974 ? 21 = 999

г) 127 ? 838 ? 659 = 306

д) 836 ? (468 ? 112) = 480

е) 986 ? 962 ? 879 = 903

ж) 625 ? (506 ? 40) = 79

з) 980 ? (350 ? 10) = 28

 

13. Как нужно расставить скобки, чтобы получить верное равен­ство:

а) 3248 : 16 – 3 · 315 – 156 · 2 = 600;

б) 350 – 15 · 104 – 1428 : 14 = 320?

14. Перед вами числовой коврик. В клеточке со зна­ками вопросов впишите пропущенные цифры и решите 8 примеров.

15. Расставьте знаки действий и скобки так, чтобы получилось верные равенства:

728 72 8 = 152

728 72 8 = 719

728 72 8 = 100

728 72 8 = 737

16. Расставьте скобки так, чтобы получить верные равенства:

40 : 8 + 2 · 6 = 2

40 : 8 + 2 · 6 = 24

40 : 8 + 2 · 6 = 17

40 : 8 + 2 · 6 = 42

17. Расставьте знаки действий и скобки так, чтобы получились заданные числа:

1 2 3 4 = 0

1 2 3 4 = 5

1 2 3 4 = 28

1 2 3 4 = 36

18. Расставьте знаки действий и скобки так что бы получились верные равенства:
 

5 7 12 21 = 74

18 11 5 19 = 103

37 5 22 15 = 72

64 7 1 19 = 152

19. В записи 1 * 2 * 3 * 4 * 5 = 100 замените каждую из звездочек знаками арифметических действий и расставьте скобки так, чтобы получилось верное равенство.

СКОЛЬКО ФИГУР НА РИСУНКЕ

1. Сколько перед вами квадратов?
2. Сколько всего треугольников изображено на рисунке?
3. Сосчитай, сколько всего треугольников изображено на рисунке?
4. Сосчитай, сколько прямоугольников изображено на рисунке?
5. Сосчитай, сколько прямоугольников изображено на рисунке?

6. Мозаика из квадратов. На рисунках вы видите мозаику из квадратов. Внимательно рассмотрите ее и сосчитайте:

а) сколько квадратов изображено в первом моза­ичном рисунке? (рис. а)

б) сколько квадратов и прямоугольников во вто­рой мозаике? (рис. б)

а) б)

7. Геометрический коврик. Сколько треугольников, ромбов и параллело­граммов изображено на рисунке?

8. Орнамент на плитке. На керамической плитке изображены шести­угольники из треугольников. Определите, сколько треугольников (разных по площади) можно сосчи­тать на рисунке?

9. Трапеции и треугольники. На рисунке изображены трапеции, решетка с центральной линией, треугольник с двумя медиа­нами и мексиканская шляпа из треугольников.

а) б)

в) г)

Сосчитайте, сколько всего трапеций и треуголь­ников изображено в каждом рисунке?

10. Геометрические фигуры из треугольников. На рисунке изображены состоящие из треуголь­ников: равносторонний треугольник, геометриче­ский гриб, мельница, пятиконечная звезда и шес­тиугольник.

а) б) в)

г) д)

Сосчитайте, сколько треугольников в каждой фигуре?

11. Треугольники (Задача-шутка). Сколько треугольников вы видите на рисунке?

а) б)

12. Сколько треугольников изображено на рисунке?

а) б)

14. Сколько треугольников изображено на рисунках?

а) б) в)

15. Сколько квадратов и треугольников изображено на рисунках?

а) б)

16. Сколько треугольников изображено на рисунке?

а) б) в)

17. Сколько квадратов изображено на рисунке?

а) б) в)

18. Сколько четырехугольников изображено на рисунке?

а) б) в)

19. Сколько треугольников изображено на рисунке?

а) б) в)

Определение, Как найти делители числа?, Примеры

Фактор — это латинское слово, означающее «действующий», «творец» или «исполнитель». Множитель числа в математике — это число, которое делит данное число. Следовательно, множитель есть не что иное, как делитель данного числа. Чтобы найти множители, мы можем использовать метод умножения, а также метод деления. Мы также можем применить правила делимости.

Факторинг — это полезный навык для поиска факторов, который в дальнейшем используется в реальных жизненных ситуациях, таких как деление чего-либо на равные части или деление на строки и столбцы, сравнение цен, обмен денег и понимание времени, а также выполнение расчетов во время путешествий. .

Что такое факторы?

В математике множитель — это число, которое делит другое число нацело, то есть без остатка. Множители также могут быть алгебраическими выражениями, равномерно делящими другое выражение. Что ж, множители и множители являются частью нашей повседневной жизни, от раскладывания вещей, таких как сладости в коробке, обращения с деньгами, до поиска закономерностей в числах, решения отношений и работы с дробями.

Определение фактора

Множитель — это число, на которое данное число делится без остатка.Факторы числа могут называться числами или алгебраическими выражениями, которые без остатка делят данное число/выражение. Делители числа могут быть как положительными, так и отрицательными.

Например, давайте проверим множители числа 8. Поскольку 8 можно разложить на множители как 1 × 8 и 2 × 4, а мы знаем, что произведение двух отрицательных чисел является только положительным числом. Следовательно, множители 8 на самом деле равны 1, -1, 2, -2, 4, -4, 8 и -8. Но когда дело доходит до задач, связанных с факторами, учитываются только положительные числа, то есть целое число и не дробное число.

Свойства факторов

Факторы числа обладают определенным набором свойств. Ниже приведены свойства факторов:

• Количество множителей числа конечно.
• Коэффициент числа всегда меньше или равен заданному числу.
• Каждое число, кроме 0 и 1, имеет как минимум два делителя: 1 и само себя.
• Деление и умножение — это операции, используемые при нахождении множителей.

Как найти делители числа?

Мы можем использовать как « Деление », так и « Умножение », чтобы найти множители.

Факторы по подразделениям

Чтобы найти делители числа с помощью деления:

• Найдите все числа, меньшие или равные заданному числу.
• Разделите заданное число на каждое из чисел.
• Делители, при которых остаток равен 0, являются делителями числа.

Пример: Найдите положительные множители числа 6 с помощью деления.

Решение:

Положительные числа, которые меньше или равны 6, это 1, 2, 3, 4, 5 и 6. Разделим 6 на каждое из этих чисел.

Мы можем заметить, что делители 1, 2, 3 и 6 дают ноль в остатке. Таким образом, множители 6 равны 1, 2, 3 и 6.

Коэффициенты умножения

Чтобы найти множители с помощью умножения:

Пример: Найдите положительные множители числа 24 с помощью умножения.

Решение:

Мы запишем 24 как произведение двух чисел несколькими способами.

Все числа, которые участвуют в этих произведениях, являются делителями данного числа (по определению множителя числа)

Таким образом, множители числа 24 равны 1, 2, 3, 4, 6, 8, 12 и 24.

Нахождение числа факторов

Мы можем найти количество множителей заданного числа, используя следующие шаги.

• Шаг 1: Найдите его простую факторизацию, т. е. выразите его как произведение простых чисел.
• Шаг 3: Запишите простую факторизацию в форме экспоненты.
• Шаг 3: Добавьте 1 к каждому показателю степени.
• Шаг 4: Перемножьте все полученные числа. Это произведение даст количество факторов заданного числа.

Пример: Найдите количество делителей числа 108.

Решение:

Выполнить простую факторизацию числа 108:

Таким образом, 108 = 2 × 2 × 3 × 3 × 3.В экспоненциальной форме: 108 = 2 ² × 3 ³ . Добавьте 1 к каждому из показателей степени, 2 и 3, здесь. Тогда 2 + 1 = 3, 3 + 1 = 4. Умножьте эти числа: 3 × 4 = 12. Таким образом, число множителей 108 равно 12.

Фактические делители числа 108 равны 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54 и 108. Здесь 108 имеет 12 делителей, и, следовательно, наш приведенный выше ответ верен.

Алгебра-Факторы

Факторы существуют и для алгебраического выражения. Например, коэффициенты 6х равны 1, 2, 3, 6, х, 2х, 3х и 6х.Существуют различные типы процедур для поиска факторов в алгебре. Вот некоторые из них:

Мы узнаем об этих видах факторинга в старших классах. Нажмите на приведенные выше ссылки, чтобы подробно изучить каждую из них.

Факторы чисел

Ниже приведен список тем, тесно связанных с Факторами. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.

Часто задаваемые вопросы о факторах

Что такое факторы в математике?

Множитель — это число, на которое данное число делится без остатка.Делители числа могут быть как положительными, так и отрицательными. Их количество конечно. Например, множители 7 равны 1 и 7. Делители 8 равны 1, 2, 4 и 8.

Как найти количество факторов?

Мы можем найти количество множителей заданного числа, используя следующие шаги.

• Найдите его простую факторизацию, т. е. представите его как произведение простых чисел.
• Запишите простую факторизацию в форме экспоненты.
• Добавьте 1 к каждому показателю степени.
• Перемножить все полученные числа.
• Это произведение даст количество множителей заданного числа.

Что такое простая факторизация?

Разложение числа на простые множители — это его запись в виде произведения двух или более простых чисел. Например, простая факторизация 60 = 2 ² × 3 × 5,

.

Что такое формула факторов?

Формула множителей для числа дает общее количество множителей числа.Для числа N, простая факторизация которого равна X ^a × Y ^b × Z ^c , (a+1) (b+1) (c+1) — это общее количество факторов.

Как факторизовать уравнения?

Мы не можем факторизовать уравнения, но можем факторизовать выражения. Факторизация выражения — это его запись в виде произведения двух или более выражений. Например: 3x ² + 6x = 3x(x + 2)

Каковы общие делители чисел 4 и 12?

Коэффициенты 4 = 1, 2 и 4. Делители числа 12 = 1, 2, 3, 4, 6 и 12. Таким образом, общие делители числа 4 и 12 равны 1, 2 и 4.

Что такое множитель каждого числа?

Делитель числа — это число, которое полностью делится на это число. 1 делит каждое число, таким образом, 1 является множителем каждого числа.

Что такое простые делители числа?

Простой множитель числа — это множитель данного числа, которое является простым числом. Факторы — это числа, которые умножаются друг на друга, чтобы получить другое число.

Может ли 0 быть делителем любого числа?

Так как n/0 не определено для любого числа, кроме нуля. Следовательно, ноль не является множителем любого отличного от нуля числа. Кроме нуля, все целые числа являются делителями нуля, потому что 0n = 0 для всех чисел.

Math Tricks — ядро ​​исследования поведенческих наук

Эта веб-страница посвящена

невероятно умной
идее о том, что математика может быть интересной!

Попробуйте эти трюки:

Вот несколько интересных ссылок:

• Список книг по хитрой математике для чтения, большинство из которых я использовал для этого сайта.
• Узнайте об оригинальном компьютере: The Abacus (http://www.ee.ryerson.ca:8080/~elf/abacus/)
• Сыграйте в математическую игру-погоню (http://dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape, Не прокручивать страницу вниз, пока загружается .
• Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
• Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
• Проверьте свои знания таблицы умножения (http://www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.html)
• Попробуйте свои силы в оценке (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
• Исследуйте геометрию в увлекательной интерактивной форме.
• Попробуйте загадку «Ханойская башня» (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
• Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
• Посмотрите, что такое набор Мандельброта (http://www. franceway.com/java/fractale/mandel_b.htm).
• Если вы хотите больше задач по математике , попробуйте новый сайт PBS MATHLINE MATH CHALLENGES.Попробуйте, вам понравится. (Но помните, что мы были первыми.)

Волшебный трюк №1

Удивите пеонов этим. Все просто. Это эффективно. Он получает их каждый раз.

1. Спросите свою оценку по номеру выберите три (3) разных номеров от 1 до 9.
2. Скажите ему или ей (или ей или ему) записать три числа рядом друг с другом, начиная с самого большого и заканчивая наименьшим, чтобы получилось одно трехзначное число. Скажите ему/ей, чтобы он не говорил вам, что это за цифры.
3. Затем попросите ее или его составить новое трехзначное число, перевернув цифры, поставив наименьшее первым, а самое большое последним. И напишите это число прямо под первым числом.
4. Теперь попросите его или ее вычесть меньшее (и меньшее) трехзначное число из старшего (и большего) трехзначного числа. Скажи им, чтобы они не говорили тебе, каков результат.
5. Теперь у вас есть выбор оберток:
   1. Попросите вашего друга сложить три цифры числа, которое получается в результате вычитания меньшего из большего трехзначного числа.Затем удивите его или ее, сказав, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
   2. Скажите своему другу, что если он или она скажет вам, какая первая ИЛИ последняя цифра ответа, вы скажете ей или ему, какие две другие цифры. Это возможно, потому что средняя цифра всегда будет 9, а сумма двух других цифр всегда будет 9! Таким образом, чтобы получить цифру, отличную от средней (которая равна 9) и отличную от цифры, которую сказал вам ваш друг, просто вычтите цифру, которую ваш друг сказал вам, из 9, и это будет неизвестная цифра.

Наверх

Магический квадрат #15

Каждая строка и столбец в сумме дают 15 в этом магическом квадрате. Так сделайте обе диагонали!

 

Наверх

Магический квадрат #34

Каждая строка и каждый столбец в этом магическом квадрате в сумме дают 34. Так сделайте обе диагонали!

 

1	15	14	4
12	6	7	9
8	10	11	5
13	3	2	16

Наверх

Рецепт для собственного магического квадрата 3 X 3

Вот рецепт создания собственного квадрата магических чисел 3 х 3.Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски большой книги под названием « Математика на миллион » Ланселота Хогбена, изданной Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.

Некоторые необходимые правила и определения:

1. Пусть буквы a , b и c обозначают целые числа (то есть целые числа).
2. Всегда выбирайте a так, чтобы оно было больше суммы b и c .То есть a > b + c . Это гарантирует отсутствие записи в магический квадрат отрицательного числа.
3. Не допускайте 2 X b = c . Это гарантирует, что вы не получите одно и то же число в разных ячейках.
4. Используя формулы, приведенные в таблице ниже, вы можете составить магический квадрат, в котором сумма строк, столбцов и диагоналей равна 3 X независимо от и .

 

а + в	а + б — в	а — б
а — б — в	и	а + б + в
а + б	а — б + в	а — в

Чтобы создать первый магический квадрат #15 выше, пусть a будет равно 5, пусть b будет равно 3, и пусть c будет равно 1. Вот некоторые другие:

• а = 6, б = 3, в = 2
• а = 6, б = 3, в = 1
• а = 7, б = 3, в = 2
• а = 7, б = 4, в = 2
• а = 8, б = 6, в = 1
• а = 8, б = 5, в = 2
• а = 8, б = 4, в = 3

Попробуйте придумать что-нибудь свое.

Наверх

Перевернутый магический квадрат

Вот магический квадрат, который не только дает в сумме 264 по всем направлениям, но и делает это, даже когда он перевернут! Если не веришь мне, посмотри на это, стоя на голове! (Или просто скопируйте его и переверните.)

 

96	11	89	68
88	69	91	16
61	86	18	99
19	98	66	81

Наверх

Антимагический квадрат

Вот магический квадрат с максимально возможным количеством различных сумм .

 

Эта таблица дает 8 различных итоговых значений .

Наверх

Выиграйте ставки с этим Волшебным квадратом

Хорошо, вот отличный способ выиграть ставки с помощью магического квадрата. Позвоните другу по телефону. Пусть он или она возьмет карандаш и бумагу и поднесет их к телефону, чтобы он или она могли записать цифры от 1 до 9. Скажите своему другу, что вы будете по очереди называть цифры от 1 до 9. Никто из вас не может повторить номер, который называет другой.Затем вы оба записываете числа от 1 до 9. Затем, когда ваш друг называет одно из чисел, он или она обводит это число кружком, и вы тоже. Когда вы называете число, вы рисуете квадрат вокруг этого числа, и ваш друг делает то же самое. Победителем становится тот, кто первым наберет три числа, сумма которых точно равна 15.

Допустим, вы идете первым, и вы зовете 8. Ваш друг может окликнуть 6. Затем вы зовете 2. Ваш друг зовет 5, а вы зовете 4. Ваш друг зовет 7, а вы зовете 3. Затем вы говорите своему другу, что вы только что выиграли, потому что назвали 8, 3 и 4, что в сумме дает 15.

Ваш друг снова захочет поиграть. Так что на этот раз вы можете поспорить с ним, что выиграете, с условием, что в случае ничьей (когда вы используете числа от 1 до 9, но ни один из вас не получает в сумме 15) никто ничего не должен.

Если вы знаете хитрость, вы никогда не проиграете, и, вероятно, проиграете в большинстве случаев.

Фокусы На самом деле фокус основан как на крестиках-ноликах, так и на магическом квадрате.Магический квадрат выглядит так:

.

 

Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме дают 15. Так что, если этот квадрат перед вами с вашим другом по телефону, вы можете поставить X в квадраты номер, который вы называете, и O в квадратах номеров, которые называет ваш друг. Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.

Итак, в приведенном выше примере, когда вы называете 8, вы ставите X в верхнем левом углу.Когда ваш друг говорит 6, вы ставите ) в правом верхнем углу. И так далее.

Наверх

Математический карточный фокус

Для этого задания вам понадобится обычная колода карт. Никаких причудливых перетасовок не требуется. Просто следуйте этим простым шагам:

1. Перемешайте карты, чтобы тщательно их перемешать.
2. Разложите 36 карт стопкой.
3. Попросите друга выбрать одну из 36 карт, посмотреть на нее и запомнить, а затем положить ее обратно в стопку, не показывая ее вам.
4. Перемешайте 36 карт.
5. Разложите 36 карт в 6 рядов по 6 карт в каждом. Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий.
6. Попросите друга посмотреть на карточки и сказать, в каком ряду находится выбранная карточка. Запомните, под каким номером находится ряд.
7. Аккуратно поднимите карты в том же порядке, в котором вы их положили .Таким образом, первая карта слева в верхнем ряду находится наверху стопки, а последняя карта справа в нижнем ряду — внизу стопки.
8. Теперь разложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карты по одному столбцу за раз . Вместо того, чтобы переходить от одной строки к другой, переходите от одного столбца к другому. Разложите первые шесть карт в столбце сверху вниз в крайний левый угол. Затем выложите следующие шесть карт во второй столбец из шести карт справа от первого столбца из шести карт.Продолжайте делать это до тех пор, пока у вас не будет 6 столбцов по 6 карточек в каждом (что выглядит так же, как 6 рядов по 6 карточек в каждом, потому что равно ).
9. Еще раз спросите у друга, в каком ряду находится выбранная карта.
10. Когда ваш друг говорит вам, в каком ряду находится карта, вы можете сказать, что это за выбранная карта. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки.Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.

Наверх

Калькулятор молний

Вот уловка, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, пусть они заменят их на любую другую цифру от 1 до 9.Затем попросите их скопировать свои девять номеров в том же порядке рядом с исходными девятью номерами. Это даст им число с 18 цифрами, первая половина которого такая же, как вторая половина. Затем измените вторую цифру на 7 и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную.Ответ: 0 — 7 делится на это новое число ровно без остатка!

Наверх

Таблицы забавных чисел

Следующие забавные таблицы взяты из одной из моих любимых книг всех времен, Recreations in the Theory of Numbers , Альберта Х. Бейлера, опубликованной Dover Publications. Эта книга на самом деле объясняет математические причины, по которым эти трюки работают.

 

3 х 37 = 111 и 1 + 1 + 1 = 3

 

6 х 37 = 222 и 2 + 2 + 2 = 6

 

9 х 37 = 333 и 3 + 3 + 3 = 9

 

12 х 37 = 444 и 4 + 4 + 4 = 12

 

15 х 37 = 555 и 5 + 5 + 5 = 15

 

18 х 37 = 666 и 6 + 6 + 6 = 18

 

21 х 37 = 777 и 7 + 7 + 7 = 21

 

24 х 37 = 888 и 8 + 8 + 8 = 24

 

27 х 37 = 999 и 9 + 9 + 9 = 27

 

1 х 1 = 1

 

11 х 11 = 121

 

111 х 111 = 12321

 

1111 х 1111 = 1234321

 

11111 х 11111 = 123454321

 

111111 х 111111 = 12345654321

 

1111111 х 1111111 = 1234567654321

 

11111111 х 11111111 = 123456787654321

 

111111111 х 111111111=12345678987654321

 

1 х 9 + 2 = 11

 

12 х 9 + 3 = 111

 

123 х 9 + 4 = 1111

 

1234 х 9 + 5 = 11111

 

12345 х 9 + 6 = 111111

 

123456 х 9 + 7 = 1111111

 

1234567 х 9 + 8 = 11111111

 

12345678 х 9 + 9 = 111111111

 

123456789 х 9 +10 = 1111111111

 

 

9 х 9 + 7 = 88

 

98 х 9 + 6 = 888

 

987 х 9 + 5 = 8888

 

9876 х 9 + 4 = 88888

 

98765 х 9 + 3 = 888888

 

987654 х 9 + 2 = 8888888

 

9876543 х 9 + 1 = 88888888

 

98765432 х 9 + 0 = 888888888

 

1 х 8 + 1 = 9

 

12 х 8 + 2 = 98

 

123 х 8 + 3 = 987

 

1234 х 8 + 4 = 9876

 

12345 х 8 + 5 = 98765

 

123456 х 8 + 6 = 987654

 

1234567 х 8 + 7 = 9876543

 

12345678 х 8 + 8 = 98765432

 

123456789 х 8 + 9 = 987654321

 

7 х 7 = 49

 

67 х 67 = 4489

 

667 х 667 = 444889

 

6667 х 6667 = 44448889

 

66667 х 66667 = 4444488889

 

666667 х 666667 = 444444888889

 

6666667 х 6666667 = 44444448888889

 

и Т. Д.

 

4 х 4 = 16

 

34 х 34 = 1156

 

334 х 334 = 111556

 

3334 х 3334 = 11115556

 

33334 х 33334 = 1111155556

 

и Т. Д.

Наверх

Знаете ли вы…?

Каждое двузначное число, оканчивающееся на 9, является суммой двух цифр плюс сумма двух цифр. Так, например, 29 = (2 х 9) + (2 + 9). 2 х 9 = 18, 2 + 9 = 11, 18 + 11 = 29,

40 — это уникальное число, потому что, когда его записывают как «сорок», это единственное число, буквы которого расположены в алфавитном порядке.

Простое число — это целое число больше 1, которое не делится без остатка ни на какое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.

139 и 149 — первые последовательные простые числа, отличающиеся на 10.

69 — это единственное число, в котором квадрат и куб между ними используют все цифры от 0 до 9 по одному разу:
69 ² = 4761 и 69 ³ = 328 509.

Один фунт железа содержит примерно 4 891 500 000 000 000 000 000 000 атомов.

Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.

Земля проходит более полутора миллионов миль каждый день.

В Эйфелевой башне 2 500 000 заклепок.

Если бы все кровеносные сосуды в человеческом теле сложить встык, они растянулись бы на 100 000 миль.

Наверх

Математический трюк для этого года

Этот предположительно будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.

1. Выберите количество дней в неделю, когда вы хотели бы выходить на улицу (1-7).

2. Умножьте это число на 2.

3. Добавить 5.

4. Умножьте полученную сумму на 50.

5. В 1998 году, если у вас уже был день рождения в этом году, добавьте 1748. Если нет, добавьте 1747. В 1999 году просто добавьте 1 к этим двум числам (поэтому добавьте 1749, если у вас уже был день рождения, и добавьте 1748, если у вас нет). В 2000 году номер меняется на 1749 и 1748. И так далее.

6. Вычтите из четырех цифр год своего рождения (19XX).

Результаты:

У вас должно быть трехзначное число.

Первая цифра этого числа — это количество дней, в течение которых вы хотите выходить на улицу каждую неделю (1–7).

Последние две цифры — ваш возраст.

(Спасибо, что передала мне это, Джуди.)

Наверх

Где струна?

В следующий раз, когда вы будете с группой людей и захотите произвести на них впечатление своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до любого числа.Возьмите кусок веревки и скажите, чтобы он привязал ее кому-нибудь к пальцу, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто посчитают за вас и дадут вам ответы. Затем попросите одного из них ответить на следующие вопросы:

1. Умножить номер человека со строкой на 2.

2. Добавить 3.

3. Умножьте результат на 5.

4. Если строка находится справа, добавьте 8.

Если строка находится слева, добавьте 9.

5. Умножить на 10.

6. Добавьте номер пальца (большой палец = 1).

7. Добавить 2.

Попросите их сказать вам ответ. Затем мысленно вычтите 222. Остаток дает ответ, начиная с правой цифры ответа.

Например, предположим, что струна находится на безымянном пальце левой руки Игрока №6:

1. Умножить на 2 = 12.

2. Прибавить 3 = 15.

3.Умножить на 5 = 75.

4. Поскольку нить находится слева, прибавьте 9 = 84.

5. Умножить на 10 = 840.

6. Прибавляем номер пальца (3) = 843.

7. Прибавить 2 = 845.

Теперь мысленно вычтите 222 = 623. Цифра справа (3) говорит о том, что струна находится на безымянном пальце. Средняя цифра говорит о том, что он находится на левой руке (правая рука = 1). Цифра слева говорит о том, что строка принадлежит Игроку №6.

Кстати, когда номер человека больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ левые цифры будут номером Игрока.

В чем секрет?

(Это из замечательной книги под названием Giant Book of Puzzles & Games, Шейлы Энн Бэрри. Издана Sterling Publishing Co., Inc., Нью-Йорк, 1978 г., недавно переиздана в мягкой обложке.)

Оставайтесь с нами, чтобы узнать больше о математических трюках. Они будут добавляться время от времени, так что не забудьте проверить снова.

Что такое произведение в математике? — Определение и обзор — Видео и стенограмма урока

Как найти произведение

Умножение часто называют повторным сложением , потому что задача умножения говорит вам о том, что у вас есть определенное количество групп чего-то, каждая из которых содержит определенное число.Еще не запутались? Вот пример.

У вас есть 3 пакета конфет, в каждом пакете 5 конфет. Сколько у тебя конфет?

Есть два способа решить эту проблему. Первый — сложить конфеты:

5 + 5 + 5 = 15

Другой способ решить — использовать умножение, потому что у вас есть 3 группы конфет по 5 штук в каждом мешочке.

3 * 5 = 15

Ответом на эту задачу на умножение является произведение, которое в данном случае равно 15.

Вот еще пример. В классе 8 рядов стульев, в каждом ряду по 7 стульев. Сколько здесь стульев?

Опять же, вы можете добавить:

7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 56

Или вы можете найти произведение, умножив:

7 * 8 = 56

Свойства Умножение

Есть четыре основных свойства умножения, которые верны независимо от того, что перемножается.

1. Коммутативное свойство : При умножении двух чисел произведение будет одинаковым независимо от порядка их записи.

Например:

5 * 7 = 7 * 5

2. Ассоциативное свойство : При умножении трех или более чисел результат будет одинаковым, независимо от того, какие два числа умножаются первыми.

Например:

(2 * 4) * 6 = 2 * (4 * 6)

8 * 6 = 2 * 24

48 = 48

3. Свойство мультипликативной идентичности : Произведение любого число и 1 это число.

Например:

3 * 1 = 3

4. Распределительное свойство : Сумма двух чисел, умноженных на третье число, равна сумме каждого слагаемого, умноженного на третье число.

Например:

2 * (3 + 4) = 2 * 3 + 2 * 4

2 * 7 = 6 + 8

14 = 14

Специальные продукты

Следует упомянуть два специальных продукта.

1. Произведение любого числа, умноженного на 1, есть это число. Вы узнали об этом в примере с мультипликативным свойством идентичности выше.

Например:

7 * 1 = 7

2,376 * 1 = 2,376

2. Произведение любого числа, умноженного на 0, равно 0.

Например:

9 * 0 = 0 9 = 0

Резюме урока

Произведение является ответом на задачу умножения. Вы можете найти продукт с помощью процесса, называемого повторным сложением , то есть путем суммирования количества групп в задаче. Есть четыре свойства, которые определяют правила решения задач на умножение: коммутативное , ассоциативное , мультипликативное тождество и дистрибутивное .Есть также два специальных правила произведения: произведение любого числа, умноженного на единицу, будет этим числом, а произведение любого числа, умноженного на ноль, будет равно нулю.

Поиск продукта

• Произведение является ответом на задачу на умножение.
• Чтобы найти продукт, вы можете использовать многократное сложение или умножение.
• Задачи на умножение обладают четырьмя свойствами: коммутативным, ассоциативным, мультипликативным, тождественным и дистрибутивным.
• Любое число, умноженное на 1, равно самому себе, а любое число, умноженное на 0, равно 0.

Результаты обучения

Изучите этот урок, чтобы точно выполнить следующие действия:

• Распознать произведение задачи на умножение
• Продемонстрировать два метода поиска продукта
• Перечислить четыре свойства умножения
• Расчет специальных продуктов

Учебный продукт простых множителей

Теория чисел , или изучение целых чисел (счетные числа 1, 2, 3. .., их противоположности –1, –2, –3… и 0), годами очаровывал математиков. Простые числа — понятие, знакомое большинству учащихся 4-х классов и старше, — основа теории чисел. Они образуют основные строительные блоки для всех целых чисел.

Простое число — это счетное число, имеющее только два делителя: само себя и единицу. Счетные числа, имеющие более двух делителей (например, 6, чьи делители равны 1, 2, 3 и 6), называются составными числами . Число 1 имеет только один делитель и обычно не считается ни простым, ни составным.

• Ключевой стандарт: определить, является ли заданное число простым или составным, и найти все множители для целого числа. (Класс 4)

Почему важны простые факторы?

Это извечный вопрос, с которым приходится сталкиваться учителям математики во всем мире. Когда я буду это использовать? Одним из ярких примеров является криптография , или изучение создания и расшифровки кодов. С помощью компьютера легко умножить два простых числа.Однако может быть чрезвычайно трудно разложить число на множители. Из-за этого, когда веб-сайт безопасно отправляет и получает информацию — что особенно важно, например, для финансовых или медицинских веб-сайтов — вы можете поспорить, что за кулисами находятся простые числа. Простые числа также проявляются в самых разных неожиданных контекстах, включая физику, музыку и даже появление цикад!

Есть еще одно место, где часто встречаются простые числа, и его легко не заметить при обсуждении приложений: математика! Изучение чистой математики — это тема, которую люди практикуют, изучают и делятся, не беспокоясь о том, где еще она может применяться, подобно тому, как музыканту не нужно спрашивать, как музыка применима к реальному миру.Теория чисел — чрезвычайно богатая тема, занимающая центральное место в курсах колледжей, исследовательских работах и ​​других разделах математики. Математики всех мастей, без сомнения, много раз сталкиваются с теорией чисел в своих академических и профессиональных путешествиях.

Факториалы и нули в конце

Факториалы и завершающие нули Вы, наверное, читаете эту страницу, потому что вам дали, казалось бы, невыполнимое задание, что-то вроде «Вот очень большое число; подумайте его гораздо больший факториал, а затем выяснить, сколько нулей в конец умноженного факториала.» Это «конечные нули в упражнении «факториал» довольно легко ответить, как только вы подумаете об этом правильно. В инете ничего полезного не нашел поэтому вот небольшой урок о том, как справиться с этим. Найдите количество нули в конце расширения 23! Если я попытаюсь подключить это в мой калькулятор, я получу что-то в экспоненциальном представлении, потому что ответ слишком велик для отображения калькулятором. С практической точки зрения, калькулятор покажет мне начало числа, и я только заботясь о конце числа («конечная» часть). Так что калькулятор не поможет. Я попробую расширить факториал: 1×2×3×4×5×6×7×8×9×10×11×12×13×14×15×16×17×18×19×20×21×22×23 Я знаю, что номер получает ноль в конце, если число имеет множитель 10.Например, 10 — это коэффициент 50, 120, и 1234567890. Поэтому мне нужно выяснить, сколько раз 10 является фактором расширения 23!. Но так как 5х2 = 10, мне нужно учитывать для всех произведений 5 и 2. Глядя на факторы в приведенном выше расширении, можно увидеть гораздо больше цифр. которые кратны 2 (2, 4, 6, 8, 10, 12, 14,…), чем кратны 5 (5, 10, 15,…). То есть, если я возьму все числа с 5 в качестве множителя, у меня будет более чем достаточно четных чисел для пары. их, чтобы получить коэффициенты 10 (и еще один конечный нуль в моем факториале). Итак, чтобы найти число умножить на 10 — это множитель, все, о чем мне действительно нужно беспокоиться, это сколько раз 5 является множителем во всех числах от 1 до 23. Сколько чисел, кратных 5, находится между 1 и 23? Есть 5, 10, 15, и 20, для четырех кратных 5.В паре с 2-мя из четных множителей это дает четыре множителя по 10, так: Найдите количество завершающие нули в 101! Хорошо, сколько кратно из 5 есть в числах от 1 до 101? Есть 5, 10, 15, 20, 25,… О, черт возьми; давай сделаем это короткий путь: 100 является ближайшим кратным 5 ниже 101, и 100 ÷ 5 = 20, поэтому являются двадцатью кратными 5 от 1 до 101. Но подождите: 25 — это 5×5, поэтому каждое число, кратное 25, имеет дополнительный коэффициент 5, который мне нужно учитывать. Сколько чисел, кратных 25, находится между 1 и 101? С 100 ÷ 25 = 4, есть четыре кратных 25 от 1 до 101. Добавляя их, я получаю 20+ 4 = 24 нулей в конце числа 101! Это рассуждение распространяется работать с большими числами. Найдите количество нули в конце расширения 1000! Хорошо, есть 1000 ÷ 5 = 200 кратных из 5 от 1 до 1000. Следующая степень 5, а именно 25, имеет 1000 ÷ 25 = 40 кратных от 1 до 1000. Следующая степень 5, а именно 125, также впишется в расширение и имеет 1000 ÷ 125 = 8 кратных от 1 до 1000. Следующая степень 5, а именно 625, также вписывается в расширение и имеет 1000 ÷ 625 = 1,6… гм, хорошо, 625 имеет 1 кратное от 1 до 1000. (Меня не волнуют «кратные» 0,6, только одно полное кратное, поэтому я усекаю свой деление до целого числа.) Всего у меня 200 + 40 + 8 + 1 = 249 копий фактора 5 в расширении, и, таким образом: Предыдущий пример подчеркивает общий метод ответа на этот вопрос, независимо от того, какой факториал они дают вам. Возьмите число, которое вам дан факториал. Разделить на 5; если вы получаете десятичную дробь, усеките ее до целого числа. Разделить на 5 2 = 25; если вы получите десятичная дробь, усеченная до целого числа. Разделить на 5 3 = 125; если вы получите десятичная дробь, усеченная до целого числа. Продолжайте со все более высоким степени 5, пока в результате деления не получится число меньше 1. Если деление меньше 1, останавливаться. Суммируйте все целые числа вы попали в свои дивизии.Это количество завершающих нулей. Вот как происходит процесс работ: Сколько нулей в конце будет найдено в 4617! , при расширении? Я применю процедуру сверху: Кстати, можно получить тот же результат, , если вы будете отслеживать по ходу дела, просто многократно деля в калькуляторе по 5: 4617 ÷ 5 = 923.4 (запишите 923), 923,4 ÷ 5 = 184,68 (запишите 184), 184,68 ÷ 5 = 36,936 (запишем 36), 36,936 ÷ 5 = 7,3827 (запишите 7), 7,3827 ÷ 5 = 1,47744 (запишем 1), и 1,47744 ÷ 5 собирается быть меньше 1, так что вы сделали. Обратитесь к своей бумаге для заметок, где вы записали целые числа и сложите их, чтобы получить 1151. Примечание. Программное обеспечение, такое как Excel не поможет с такими вычислениями, не больше, чем ваш калькулятор было бы. Программное обеспечение обычно хранит только пятнадцать или около того цифр «точности», вот почему, когда число становится достаточно большим, дисплей переключается автоматически в экспоненциальное представление. Поскольку программа только хранит первые несколько начальных цифр, остальные конечные цифры должны быть заполнены нулями.Если вы попытаетесь выполнить первое раскрытие выше, «23!», в Excel, вы получите что-то с большим количеством нулей, чем на самом деле. Другими словами, компьютер даст вам неверный ответ. Так что учитесь концепции; не пытайтесь обмануть с программным обеспечением. Топ  | Вернуться к индексу Процитировать эту статью как: Стапель, Элизабет. «Факториалы и конечные нули». Пурпурная математика . Доступно с https://www.purplemath.com/modules/factzero.htm . Доступ [Дата] [Месяц] 2016

Этот урок можно распечатать для личного пользования.

Математические карточки | Quizlet

Если у вас есть два набора x и y (1,-3), (2, 4), вы всегда можете построить линию.Все, что вам нужно, это два набора точек.

Любая горизонтальная линия имеет твердую ось Y (ось Y никогда не изменяется, но ось X меняется), поэтому y = k всегда.
Любая вертикальная линия имеет фиксированную ось X, которая не изменяется, поэтому X=K

Любые две точки, имеющие одну и ту же координату Y, должны быть горизонтальной линией.
Любые две точки, имеющие одну и ту же координату x, должны быть вертикальной линией.

Наклон 2 (m = 2) может означать (-2, -1), потому что если вы разделите -2/-1 = 2. Или это может означать (2,1)

Если дано два набора точек и вы хотите найти наклон, вычтите оба Y как ваш «подъем» и вычтите оба x как ваш «бег» для подъема / пробега.

Если у вас наклон равен 2, это означает, что каждый раз, когда вы добавляете x (или -x) к координате x, вы добавляете 2 к координате y. Итак, если у вас есть точки (-3,-1), то (-2, 1) тоже должна быть координатой.

Наклон -2/3 также может означать 1 единицу влево и 2/3 единицы вверх (-1 + 2/3)

Линии с наклоном 1 или -1 образуют угол 45 градусов. Таким образом, угол, который они образуют, равен 45, 45, 90.

Параллельные прямые имеют одинаковый наклон. Перпендикулярные линии имеют наклоны с противоположными знаками (-1 и 1, и вы переворачиваете числа), поэтому наклон -(1/2) становится наклоном положительных 2 для обратной величины. Неважно, чему равно b, только наклону.

Только линии, которые пересекаются в начале координат, имеют ось x и y, равную 0.
x-intercept — точка пересечения линии с осью x, y — точка пересечения, когда y пересекает ось y. Когда задано уравнение, чтобы найти x, мы подставляем y=0, когда мы хотим найти y, мы подставляем x=0.

Точки пересечения можно классифицировать как точки: (s, 0) = пересечение по оси x, (0,S) можно классифицировать как пересечение по оси y;.

Координата x любой точки пересечения с y всегда равна 0.
Чтобы найти значение y, всегда заменяйте x на 0!

Если нам дали точку (0, 2m) и попросили заполнить y=mx+b.Мы знаем, что b равно 2 м, так как 2 м является точкой пересечения с осью y, когда x = 0.

Каждый раз, когда y проходит через начало координат, ось y будет равна 0.

Чтобы найти наклон линии с координатами (7, -4), которая проходит через происхождение. Считайте (0, 0) вторым набором баллов и сделайте рост (0 — (-4) — пробег (0 — 7) = 4/-7

Оценка при умножении

Это полный урок с инструкциями и упражнениями по использованию оценки в умножении, предназначенный для 5-го или 6-го класса. Чтобы оценить, учащиеся округляют двух- и трехзначные числа перед умножением, но это округление может быть выполнено несколькими различными способами. Далее следуют различные упражнения и текстовые задачи.

Для оценки результата умножения (произведения) округлить числа до некоторые близкие числа, которые вы можете легко умножить в уме. Одним из методов оценки является округление всех факторы до наибольшей цифры (разрядного значения), которую они имеют. (Это несколько грубый метод, но служит отправной точкой балл в оценке обучения.) Например, оценка 365 × 24 . Округлите 365 до ближайшего сто и 24 до ближайших десяти. Итак, 365 ≈ 400, а 24 ≈ 20. Тогда 365 × ​​ 24 ≈ 400 × 20 = 8000. Таким образом, умножение легко выполнить, поскольку это всего лишь одна цифра (4), умноженная на одну цифру (2), и добавление нулей в конец (000). Посмотрите другие примеры: Оценка 133 × 27 ≈ 100 × 30 = 3000 На самом деле: 2 2   133 ×   27 931 2660 3591 Оценка 79 × 73 ≈ 80 × 70 = 5600 На самом деле: 6 2   79 ×   73 237 5530 5767

Практика

1. Оцените продукты, округлив множители до наибольшего разряда. ценность.

а. 158 × 32 ≈ 200 × 30 = 6000	в. 29 × 94 ≈ ____ × ___ = ____
д. 770 × 33 ≈ ____ × ___ = ____	ф. 88 × 99 ≈ ____ × ___ = ____
Дж.486 × 21 ≈ ____ × ___ = ____	л. 209 × 27 ≈ ____ × ___ = ____

 

2. Одной из целей оценки является обнаружение грубых ошибок в расчеты. Например, если вы оцениваете результат как 5000, и вы подсчитайте, что это 354, вы знаете, что что-то не так, так как вы далеко.
Какова наилучшая оценка предложенных вариантов?

1.103 × 52 2.     42 × 76 3.    319 × 25 4.    17 × 17 5.    99 × 59 6.    47 × 21

а. 6500 а. 4000 а. 6000 а. 1000 а. 6000 а. 470

б. 500 б. 320 б. 750 б.200 б. 900 б. 9700

с. 5000 в. 4800 в. 9000 в. 400 в. 9000 в. 1000

 

3. Какой продукт дальше всего соответствует своей оценке? Может понимаешь почему?

Оценки: 236 × 28 ≈ 198 × 28 ≈ 246 × 28 ≈ 178 × 28 ≈ Точные продукты: 236 × 28 = 198 × 28 = 246 × 28 = 178 × 28 =

Другие методы оценки Когда вы округляете оба множителя до наибольшего разряда, 249 × ​​ 34 оценивается как 6000; но фактический продукт 8466 — довольно далеко от оценки. Вы получите гораздо лучшую оценку, если округлите 249 до 250 и не до 200. Округлите 34 до 30. Итак, 249 × 34 ≈ 250 × 30. Чтобы вычислить это, сначала возьмите 3 × 25 = 25 + 25 + 25 = 75, а затем добавьте к нему два нуля: 250 × 30 = 30 × 250 = 7500. Таким образом, вместо округления до ближайшей сотни можно округлить до «середина пятидесяти», если число близко к этому. Или, даже если число исчисляется сотнями, можно округлить до ближайшего десять.Например, 178 × 28 лучше оценивать как 180 × 30 — округление обоих чисел до десятых. Что вы можете сделать мысленно пройдя 100 × 30 + 80 × 30, что составляет 3000 + 2400 = 5400. Вы также можете попытаться учесть ошибку в вашей оценке округляя один множитель в большую сторону, другой в меньшую — особенно если приходится раунд один фактор много. Например, 144 × 24. Если округлить 144 до 100, округлить 24 до до 30, чтобы компенсировать некоторые ошибка. Оценка — это не точная наука, а вопрос округления до конца цифры, которые вы можете работать в вашей голове.

4. Сначала оцените, а затем рассчитайте фактический продукт. Ты сможешь используйте различные способы оценки по своему усмотрению. Или попробуйте два разных метода оценки и сравнения, который был более точным.

	Оценки:	Реальность:
а.	143 × 27 ≈  ________ × _________ = __________	143 × 27 = _________
б.	657 × 13 ≈  ________ × _________ = __________	657 × 13 = _________
в.	411 ×  9  ≈  ________ × _________ = __________	411 ×   9  = _________
я.	406 × 19 ≈  ________ × _________ = __________	406 × 19 = _________
к.	243 × 24 ≈  ________ × _________ = __________	243 × 24 = _________
л.	37 × 258 ≈  ________ × _________ = __________	37 × 258 = _________

 

5.Решите задачи со словами. При необходимости округлить числа, чтобы сделать оценку.

а.   Нелли пересчитала спички в спичечном коробке и получила 58.
Сколько спичек приблизительно в 8 коробках?

     Каждый день Нелли использует 10 спичек. Как долго примерно Хватит ли ей этих 8 коробок?

б.   Куры тети Джини несут около 130 яиц в день.
Сможет ли она поставить все яйца для вышеуказанной школы в течение одной недели?
Обратите внимание, ее куры несут яйца 7 дней в неделю.